(本小题满分14分)如图,在四棱锥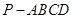 中,平面
中,平面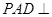 平面
平面 ,
,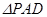 为等边三角形,底面
为等边三角形,底面 为菱形,
为菱形,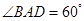 ,
, 为
为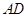 的中点,
的中点, 。
。
(1)求证: 平面
平面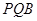 ;
;
(2) 求四棱锥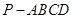 的体积
的体积
(3)在线段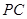 上是否存在点
上是否存在点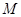 ,使
,使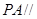 平面
平面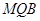 ; 若存在,求出
; 若存在,求出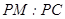 的值。
的值。
已知以向量v=(1,  )为方向向量的直线l过点(0,
)为方向向量的直线l过点(0,  ),抛物线C:
),抛物线C: (p>0)的顶点关于直线l的对称点在该抛物线上.
(p>0)的顶点关于直线l的对称点在该抛物线上.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若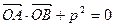 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程.
已知A,B是抛物线 上的两个动点,
上的两个动点,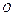 为坐标原点,非零向量
为坐标原点,非零向量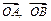 满足
满足 .
.
(Ⅰ)求证:直线 经过一定点;
经过一定点;
(Ⅱ)当 的中点到直线
的中点到直线 的距离的最小值为
的距离的最小值为 时,求
时,求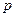 的值.
的值.
双曲线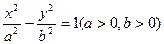 的左、右焦点分别为F1、F2,O为坐标原点,点A在双曲线的右支上,点B在双曲线左准线上,
的左、右焦点分别为F1、F2,O为坐标原点,点A在双曲线的右支上,点B在双曲线左准线上,
(1)求双曲线的离心率e;
(2)若此双曲线过C(2,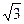 ),求双曲线的方程;
),求双曲线的方程;
(3)在(2)的条件下,D1、D2分别是双曲线的虚轴端点(D2在y轴正半轴上),过D1的直线l交双曲线M、N, 的方程。
的方程。
已知抛物线C: 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设直线 与抛物线C交于两点
与抛物线C交于两点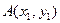 ,
, ,且
,且 (
( ,且
,且 为常数).过弦AB的中点M作平行于
为常数).过弦AB的中点M作平行于 轴的直线交抛物线于点D,连结AD、BD得到
轴的直线交抛物线于点D,连结AD、BD得到 .
.
(1)求证: ;
;
(2)求证: 的面积为定值.
的面积为定值.
设椭圆 :
: 的离心率为
的离心率为 ,点
,点 (
(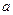 ,0),
,0), (0,
(0, ),原点
),原点 到直线
到直线 的距离为
的距离为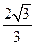 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设点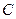 为(
为(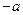 ,0),点
,0),点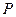 在椭圆
在椭圆 上(与
上(与 、
、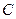 均不重合),点
均不重合),点 在直线
在直线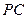 上,若直线
上,若直线 的方程为
的方程为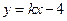 ,且
,且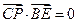 ,试求直线
,试求直线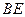 的方程.
的方程.