（本小题满分14分）
如图：某污水处理厂要在一个矩形污水处理池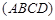
的池底水平铺设污水净化管道
，
是直角顶点）来处理污水，管道越短，铺设管道的成本越低.设计要求管道的接口是
的中点，
分别落在线段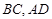
上。已知
米，
米，记
。
（Ⅰ）试将污水净化管道的长度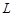
表示为
的函数，并写出定义域；
（Ⅱ）若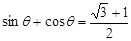
，求此时管道的长度；
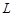（Ⅲ）问：当取何值时，铺设管道的成本最低？并求出此时管道的长度。
(本小题满分13分)
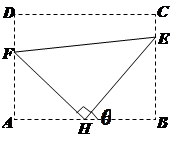
如图，矩形
所在的平面与平面
垂直，且
，
，
，
分别为
的中点．
（Ⅰ） 求证：直线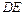
与平面
平行；
（Ⅱ）若点
在直线
上，且二面角
的大小为
，试确定点的位置．
(本小题
满分13分)
已知函数
在
处取得最值．
（Ⅰ）求函数
的最小正周期及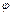
的值；
（Ⅱ）若数列
是首项与公差均为
的等差数列，求
的值．
4-5（不等试证明）
已知
（Ⅰ）若
的取值范围；
（Ⅱ）若不等式
的解集为R，求实数
的取值范围。
（（本小题满分10分）4-4（坐标系与参数方程）
已知曲线
与直线
为参数）相切，求实数
的值。
（本小题满分10分）4-1（几何证明选讲）
如图，已知BA是
的直径，AD是
O的切线，割线BD、BF分别交O于C、E，连结AE、CE。
（Ⅰ）求证：C、E、F、D四点共圆；
（Ⅱ）求证：