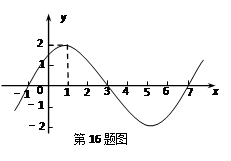近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| |
“厨余垃圾”箱 |
“可回收物”箱 |
“其他垃圾”箱 |
| 厨余垃圾 |
400 |
100 |
100 |
| 可回收物 |
30 |
240 |
30 |
| 其他垃圾 |
20 |
20 |
60 |
(1)试估计厨余垃圾投放正确的概率;
(2)试估计生活垃圾投放错误的概率;
本题满分13分）已知函数
．
（I）当
时，求函数
的单调区间；
（II）若函数
的图象在点
处的切线的倾斜角为
，问：m在什么范围取值时，对于任意的
，函数
在区间
上总存在极值？
如图:
O方程为
，点P在圆上，点D在x轴上，点M在DP延长线上，O交y轴于点N，
.且
（I）求点M的轨迹C的方程；
（II）设
，若过F1的直线交（I）中曲线C于A、B两点，求
的取值范围．
一个四棱椎的三视图如图所示：（I）求证：PA⊥BD；
（II）在线段PD上是否存在一点Q，使二面角Q-AC-D的平面角为30o？若存在，求
的值；若不存在，说明理由．
形状如图所示的三个游戏盘中（图（1）是正方形，M、N分别是所在边中点，图（2）是半径分别为2和4的两个同心圆，O为圆心，图（3）是正六边形,点P为其中心）各有一个玻璃小球，依次摇动三个游戏盘后，将它们水平放置，就完成了一局游戏．
（I）一局游戏后，这三个盘中的小球都停在阴影部分的概率是多少？
（II）用随机变量
表示一局游戏后，小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值，求随机变量的分布列及数学期望．
本题满分12分）
已知函数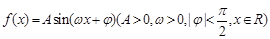
的图象的一部分如下图所示．
（I）求函数
的解析式；
（II）求函数
的最大值与最小值．