(本小题满分12分) 中,
中, 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知 满足
满足 ,且
,且
(1)求角A的大小;
(2)求 的值
的值
已知数列 是等差数列,且
是等差数列,且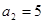 ,
, .
.
(1)求首项 及公差
及公差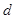 ;
;
(2)求数列 的通项公式
的通项公式 ,并问32是该数列中的第几项?
,并问32是该数列中的第几项?
在 中,
中,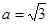 ,
, ,
, ,求角
,求角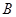 、边
、边 及
及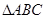 的面积
的面积 .
.
解下列不等式:
(1)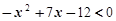 ;(2)
;(2)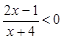 .
.
已知函数 满足
满足 , 且对于任意
, 且对于任意 恒有
恒有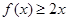 成立。
成立。
(1) 求实数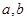 的值;
的值;
(2)设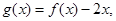 若存在实数
若存在实数 ,当
,当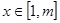 时,
时,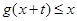 恒成立,求实数
恒成立,求实数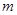 的最大值。
的最大值。
我市某蔬菜种植户计划建造一个室内面积为800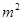 的矩形蔬菜温室,在温室内,沿左、右两侧与后侧内墙各保留1
的矩形蔬菜温室,在温室内,沿左、右两侧与后侧内墙各保留1 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 宽的空地(如图),中间部分种植蔬菜。
宽的空地(如图),中间部分种植蔬菜。
(1)当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
(2)由于受地形条件的限制,矩形温室的边长不得少于25 ,则蔬菜的最大种植面积是多少?
,则蔬菜的最大种植面积是多少?