(本小题满分12分)某公司生产陶瓷,根据历年的情况可知,生产陶瓷每天的固定成本为14000元,每生产一件产品,成本增加210元.已知该产品的日销售量 与产量
与产量 之间的关系为
之间的关系为 , 每件产品的售价
, 每件产品的售价 与产品
与产品 之间的关系为
之间的关系为
(I)写出该陶瓷厂的日销售利润 与产量
与产量 之间的关系式;
之间的关系式;
(II)若要使得日销售利润最大,每天该生产多少件产品,并求出最大利润.
(本题11分)如图,矩形ABCD中,AB=6,BC=2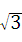 ,点O是AB的中点,点P在AB的延长线
,点O是AB的中点,点P在AB的延长线 上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点
上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点 出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积 为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;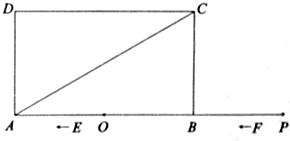
(本 题9分)已知全集
题9分)已知全集 ,集合
,集合 ,
,
集合
(1)是否存在实数 使
使 ,若存在,求出
,若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。
(2)设有限集合 ,则
,则 叫做集合
叫做集合 的和,记做
的和,记做 .若集合
.若集合 ,集合
,集合 的所有子集分别
的所有子集分别 为
为 求
求
(注: )
)
(本题共9分)如图,在△ACB中,∠AC B=90°,AC=4,BC=
B=90°,AC=4,BC= 2,点P为线段CA(不包括端点)上的一个动点,以
2,点P为线段CA(不包括端点)上的一个动点,以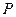 为圆心,1为半径作
为圆心,1为半径作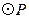 .
.
(1)连结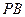 ,若
,若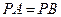 ,试判断
,试判断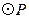 与直线AB的位置关系,并说明理由;
与直线AB的位置关系,并说明理由;
(2)当线段PC等于多少时,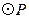 与直线AB相切?
与直线AB相切?
(3)当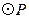 与直线AB相交时,写出线段PC的取值范围。
与直线AB相交时,写出线段PC的取值范围。
(第(3)问直接给出结果,不需要解题过程)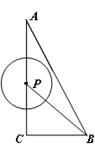
(本题9分)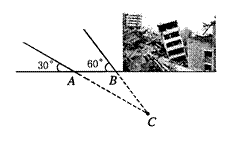
2011年3月10日,云南盈江县发生里氏5.8级地震。萧山金利浦地震救援队接到上级命令后立即赶赴震区进行救援。救援队利用生命探测仪在某建筑物废墟下方探测到点 C 处有生命迹象,已知废墟一侧地面上两探测点A、B 相距3米,探测线与地面的夹 角分别是30°和 60°(如图),试确定生命所在点 C 的深度。(结果精确到0.1米,参考数据:
角分别是30°和 60°(如图),试确定生命所在点 C 的深度。(结果精确到0.1米,参考数据: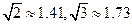 )
)
(本题9分)某校课外兴趣小组从我市七年级学生中抽取2 000人做了如下问卷调查,将统计结果绘制了如下两幅统计图

根据上述信息解答下列问题:
(1)求条形统计图中n的值.
(2)如果每瓶饮料平均3元钱,“少喝2瓶以上”按少喝3瓶计算.
①求这2000名学生一个月少喝饮料能节省多少钱捐给 希望工程?
希望工程?
②按上述统计结果估计,我市七年级6万学生一个月少喝饮料大约能节省多少钱捐给希望工程?