双曲线的离心率等于2,且与椭圆 有相同的焦点,求此双曲线方程.
有相同的焦点,求此双曲线方程.
定义在D上的函数f(x),如果满足对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界,已知函数f(x)=1+x+ax2
(1)当a=﹣1时,求函数f(x)在(﹣∞,0)上的值域,判断函数f(x)在(﹣∞,0)上是否为有界函数,并说明理由;
(2)若函数f(x)在x∈[1,4]上是以3为上界的有界函数,求实数a的取值范围.
已知函数f(x)=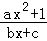 (a,b,c∈Z)是奇函数,且f(1)=2,f(2)<3.
(a,b,c∈Z)是奇函数,且f(1)=2,f(2)<3.
(1)求a,b,c的值.
(2)判断函数f(x)在[1,+∞)上的单调性,并用定义证明你的结论.
(3)解关于t的不等式:f(﹣t2﹣1)+f(|t|+3)>0.
电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间x(min)之间的关系如图所示,其中D的坐标为( ,230).
,230).
(1)若通话时间为2小时,按方案A,B各付话费多少元?
(2)方案B从500分钟以后,每分钟收费多少元?
(3)通话时间在什么范围内,方案B比方案A优惠?
已知函数f(x)是定义域在R上的奇函数,当x>0时,f(x)=x2﹣2x.
(1)求出函数f(x)在R上的解析式;
(2)写出函数的单调区间.
已知集合M={x|x2﹣3x≤10},N={x|a+1≤x≤2a+1}.
(1)若a=2,求M∩(∁RN);
(2)若M∪N=M,求实数a的取值范围.