在如图所示的几何体中,四边形
是正方形,
,
,
、
、
分别为
、
、
的中点,且
.
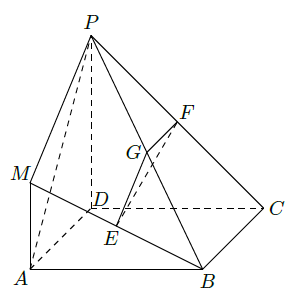
(I)求证: ;
(Ⅱ)求三棱锥 与四棱锥 的体积之比。
已知函数
(1)若 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(2)若 ,证明:
,证明:
已知数列

(I)若a1=2,证明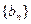 是等比数列;
是等比数列;
(II)在(I)的条件下,求 的通项公式;
的通项公式;
(III)若 ,证明数列{|
,证明数列{| |}的前n项和Sn满足Sn<1.
|}的前n项和Sn满足Sn<1.
 直角三角形
直角三角形 的直角顶点
的直角顶点 为动点,
为动点, ,
,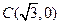 为两个定点,作
为两个定点,作 于
于 ,动点
,动点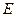 满足
满足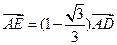 ,当点
,当点 运动时,设点
运动时,设点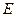 的轨迹为曲线
的轨迹为曲线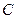 ,曲线
,曲线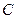 与
与 轴正半轴的交点为
轴正半轴的交点为 .
.
(Ⅰ) 求曲线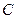 的方程;
的方程;
(Ⅱ) 是否存在方向向量为m 的直线
的直线 ,与曲线
,与曲线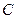 交于
交于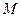 ,
,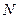 两点,且
两点,且 与
与 的夹角为
的夹角为 ?若存在,求出所有满足条件的直线方程;若不存在,说明理由.
?若存在,求出所有满足条件的直线方程;若不存在,说明理由.
过直角坐标平面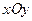 中的抛物线
中的抛物线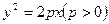 的焦点
的焦点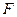 作一条倾斜角为
作一条倾斜角为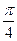 的直线与抛物线相交于A,B两点。
的直线与抛物线相交于A,B两点。
(1)用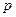 表示A,B之间的距离;
表示A,B之间的距离;
(2)证明: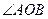 的大小是与
的大小是与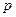 无关的定值,并求出这个值。
无关的定值,并求出这个值。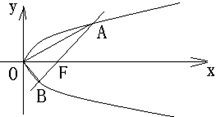
在一个圆形波浪实验水池的中心有三个振动源,假如不计其它因素,在t秒内,它们引发的水面波动可分别由函数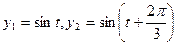 和
和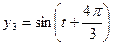 描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由
描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由