如图，已知椭圆x2a2y2b21(a<b<0)过点(1,22-优题课

题文

如图，已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 过点 $(1, \frac{\sqrt{2}}{2})$ ，离心率为 $\frac{\sqrt{2}}{2}$ ，左、右焦点分别为 $F_{1}, F_{2}$ .点 $P$ 为直线 $l : x + y = 2$ 上且不在 $x$ 轴上的任意一点，直线 $P F_{1}$ 和 $P F_{2}$ 与椭圆的交点分别为 $A, B$ 和 $C, D$ ， $O$ 为坐标原点.

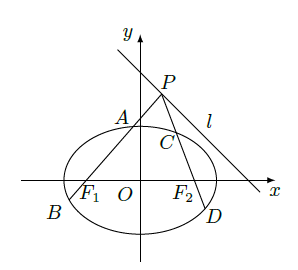
（I）求椭圆的标准方程；
（II）设直线 $P F_{1}$ 、 $P F_{2}$ 的斜线分别为 $k_{1}, k_{2}$ .
（i）证明： $\frac{1}{k_{1}} - \frac{3}{k_{2}} = 2$ ；
（ii）问直线 $l$ 上是否存在点 $P$ ，使得直线 $O A, O B, O C, O D$ 的斜率 $k_{O A}, k_{O B}, k_{O C}, k_{O D}$ 满足 $k_{O A} + k_{O B} + k_{O C} + k_{O D} = 0$ ？若存在，求出所有满足条件的点 $P$ 的坐标；若不存在，说明理由.

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

某投资公司投资甲、乙两个项目所获得的利润分别是P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式P=,Q=t,今该公司将5亿元投资于这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).求:
(1)y关于x的函数表达式.
(2)总利润的最大值.

为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,新上了把二氧化碳处理转化为一种可利用的化工产品的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为
y=
且每处理一吨二氧化碳得到可利用的化工产品价值为200元,若该项目不获利,国家将给予补偿.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则国家每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?

某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=x²+10x(万元).当年产量不小于80千件时,C(x)=51x+-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式.
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?

已知某物体的温度θ(单位:摄氏度)随时间t(单位:分钟)的变化规律是:θ=m·2^t+2^1-t(t≥0,且m>0).
(1)如果m=2,求经过多少时间,物体的温度为5摄氏度.
(2)若物体的温度总不低于2摄氏度,求m的取值范围.

已知函数f(x)=4^x+m·2^x+1有且仅有一个零点,求m的取值范围,并求出该零点.

试卷网试题网古诗词网作文网范文网