为了促进长三角区域的便捷沟通，实现节时、节能，杭州湾跨海大桥于2008年5月1日通车，下表是宁波到上海两条线路的有关数据：
| 线路 |
弯路（宁波—杭州—上海） |
直路（宁波—跨海大桥—上海） |
| 路程 |
316公里 |
196公里 |
| 过路费 |
140元 |
180元 |
（1）若小车的平均速度为80公里/小时，则小车走直路比走弯路节省多少时间？
（2）若小车每公里的油耗为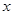
升，汽油价格为5.00元/升，问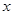为何值时，走哪条线路的总费用较少（总费用=过路费＋油耗费）；
解方程组：
（1）
（2）
已知关于x的一元二次方程x2
(2k+3)x+k2+3k+2=0
（1）试判断上述方程根的情况；
（2）若以上述方程的两个根为横坐标、纵坐标的点恰在反比例函数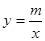
的图象上，求满足条件的m的最小值；
（3）已知△ABC的两边AB、AC的长是关于上述方程的两个实数根，BC的长为5．
①当k为何值时，△ABC是以BC为斜边的直角三角形?
②当k为何值时，△ABC是等腰三角形?请求出此时△ABC的周长．
若m为自然数，且4<m<40，且方程x2－2(2m－3)x＋4m2－14m＋8＝0的两根均为整数，求m的值．
某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放量的破裂管道有水部分的截面．
（1）请你补全这个输水管道的圆形截面；（用尺规作图，注意保留作图痕迹）
（2）若这个输水管道有水部分的水面宽AB="16" cm，水面最深地方的高度为4 cm，求这个圆形截面的半径．
已知关于x的方程a2x2+（2a－1）x+1=0有两个实数根x1，x2．（1）当a为何值时，x1≠x2；（2）是否存在实数a，使方程的两个实数根互为相反数？如果存在，求出a的值；如果不存在，说明理由．
解：（1）根据题意，得△=（2a－1）2－4a2>0，解得a<
．
∴当a<时，方程有两个不相等的实数根．
（2）存在，如果方程的两个实数根x1，x2互为相反数，则x1+x2=－
=0①，
解得a=
，经检验，a=是方程①的根．
∴当a=时，方程的两个实数根x1与x2互为相反数．
上述解答过程是否有错误？如果有，请指出错误之处，并解答．