已知关于x的方程a2x2+（2a－1）x+1=0有两个实数根x1，x2．（1）当a为何值时，x1≠x2；（2）是否存在实数a，使方程的两个实数根互为相反数？如果存在，求出a的值；如果不存在，说明理由．
解：（1）根据题意，得△=（2a－1）2－4a2>0，解得a<
．
∴当a<时，方程有两个不相等的实数根．
（2）存在，如果方程的两个实数根x1，x2互为相反数，则x1+x2=－
=0①，
解得a=
，经检验，a=是方程①的根．
∴当a=时，方程的两个实数根x1与x2互为相反数．
上述解答过程是否有错误？如果有，请指出错误之处，并解答．
已知二次函数
的图象如图所示，它 与x轴的一个交点坐标为
A（－1，0），另一交点为B，与y轴的交点坐标为C（0，3）．
（1）求出b，c的值，并写出此二次函数的解析式；
（2）求出顶点D的坐标以及
面积；
（3）根据图象，写出函数值y为正数时，自变量x的取值范围．
如图，一条河的两岸有一段是平行的，在河的南岸边每隔5米有一棵树，在北岸边每隔50米有一根电线杆．小丽站在离南岸边15米的点P处看北岸，发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住，并且在这两棵树之间还有三棵树，求河宽？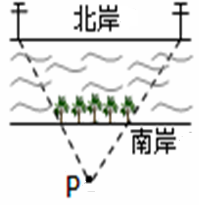
为了落实国务院惠农的指示精神，最近市政府又出台了一系列“三农”优惠政策，使农民收入大幅度增加．某农户生产经销一种农副产品，已知这种产品的成本价为20元/千克．市场调查发现，该产品每天的销售量
（千克）与销售价
（元/千克）有如下关系：
．设这种产品每天的销售利润为
（元）．
（1）求与之间的函数关系式．
（2）当销售价定为多少元时，每天的销售利润最大？最大利润是多少？
（3）如果物价部门规定这种产品的销售价不得高于28元/千克，该农户想要每天获得150元的销售利润，销售价应定为多少元？
已知格点△ABC．
（1）画出与△ABC相似的格点△A1B1C1，使△A1B1C1与△ABC的相似比为2；
（2）画出与△ABC相似的格点△A2B2C2，使△A2B2C2与△ABC的相似比为
；
今年3月5日，实验中学组织全体学生参加了“走出校门，服务社会”的活动。九年级一班小明同学统计了该天本班学生打扫街道，去敬老院服务和到社区文艺演出的人数，并做了如下直方图和扇形统计图。请根据小明同学所作的两个图形，解答：
（1）九年级一班有多少名学生？
（2）补全直方图的空缺部分。
（3）若九年级有800名学生，估计该年级去敬老院的人数。