两个全等的直角三角形ABC和DEF重叠在一起，其中∠A=60°，AC="1." 固定△ABC不动，将△DEF进行如下操作：
（1）如图1，△DEF沿线段AB向右平移（即D点在线段AB内移动），连结DC、CF、FB，四边形CDBF的形状在不断的变化，但它的面积不变化，请求出其面积.
（2）如图2，当D点移到AB的中点时，请你猜想四边形CDBF的形状，并说明理由.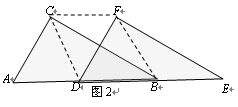
（3）如图3，△DEF的D点固定在AB的中点，然后绕D点按顺时针方向旋转△DEF，使DF落在AB边上，此时F点恰好与B点重合，连结AE，请你求出sinAED的值.
如图，E，F是四边形ABCD对角线AC上的两点，AD∥BC ，DF∥BE ，AE＝CF．
求证：（1）△AFD≌△CEB；
（2）四边形ABCD是平行四边形．
解下列一元二次方程
（1）
（2）
（1）解分式方程：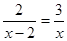
（2）如图，点A，B在数轴上，它们所对应的数分别是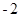
和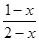
，且点A，B到原点的距离相等，求
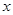的值．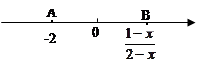
如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．
（1）证明不论E、F在BC、CD上如何滑动，总有BE=CF；
（2）当点E、F在BC、CD上滑动时，分别探讨四边形AECF和△CEF的面积是否发生变化？如果不变，求出这个定值；如果变化，求出最大（或最小）值．
某办公用品销售商店推出两种优惠方法：①购1个书包，赠送1支水性笔；②购书包和水性笔一律按9折优惠．书包每个定价20元，水性笔每支定价5元．小丽和同学需买4个书包，水性笔若干支（不少于4支）．
（1）分别写出两种优惠方法购买费用y（元）与所买水性笔支数x（支）之间的函数关系式；
（2）对x的取值情况进行分析，说明按哪种优惠方法购买比较便宜；
（3）小丽和同学需买这种书包4个和水性笔12支，请你设计怎样购买最经济．