某商场出售一批进价为2元的贺卡,在市场营销中发现商品的日销售单价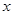 元与日销售量
元与日销售量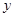 个之间有如下关系:
个之间有如下关系:
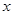 (元) (元) |
3 |
4 |
5 |
6 |
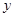 (个) (个) |
20 |
15 |
12 |
10 |
(1)根据表中数据,在直角坐标系描出实数对(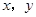 )的对应点
)的对应点
(2)猜测并确定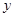 与
与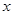 之间的函数关系式,并画出图象;
之间的函数关系式,并画出图象;
(3)设经营此贺卡的销售利润为W元,试求出W与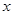 之间的函数关系式,若物价居规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价
之间的函数关系式,若物价居规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价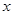 定为多少元时,才能获得最大日销售利润?
定为多少元时,才能获得最大日销售利润?
如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,且DC=BF,DE⊥CF于E,问E是CF的中点吗?试说明理由
如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90º,点D为AB边上的一点,
(1)试说明:∠EAC=∠B;
(2)若AD=10,BD=24,求DE的长.
中菲黄岩岛争端持续,我海监船加大黄岩岛附近海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,黄岩岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向黄岩岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
(1)请用直尺和圆规作出C处的位置;
(2)求我国海监船行驶的航程BC的长.
如图,四边形ABCD中,AB∥CD,AB=CD,A、F、E、C在同一直线上,
∠ABE=∠CDF.
(1)试说明:△ABE≌△CDF;
(2)试说明:AF=CE.
作图题:
(1)如图,在图1所给方格纸中,每个小正方形边长都是1,标号为①②③的三个三角形均为格点三角形(顶点在方格顶点处),请按要求将图2中的指定图形分割成三个三角形,使它们与标号为①②③的三个三角形分别对应全等.(分割线画成实线.)
(2)如图3,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
①在图中画出与△ABC关于直线L成轴对称的△A′B′C′;
②请直线L上找到一点P,使得PC + PB的距离之和最小..