某同学要把自己的计算机接入因特网,现有两家ISP公司可供选择,公司A每小时受费1.5元;公司B的收费规则如下:在用户上网的第1小时内收费1.7元,第2小时内收费1.6元,以后每小时减少0.1元(若超过17小时,按17小时计算)如图所示.
假设一次上网时间总小于17小时,那么,一次上网在多长时间以内能够保证选择公司A比选择公司B所需费用少?请写出其中的不等关系.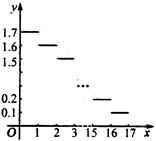
已知三条直线l1:2x-y+a =" 0" (a>0),直线l2:-4x+2y+1 = 0和直线l3:x+y-1= 0,且l1与l2的距离是 .
.
(1)求a的值;
(2)能否找到一点P,使得P点同时满足下列三个条 件:
①P是第一象限的点;
②P 点到l1的距离是P点到l2的距离的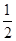 ;
;
③P点到l1的距离与P点到l3的距离之比是 ∶
∶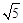 .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.
等差数列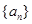 的前
的前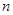 项和为
项和为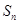 ,且
,且 .
.
(1)数列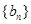 满足:
满足: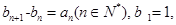 求数列
求数列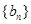 的通项公式;
的通项公式;
(2)设 求数列
求数列 的前
的前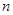 项和
项和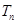
在△ABC中,角A,B,C的对边分别为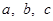 ,且A,B,C成等差数列。
,且A,B,C成等差数列。
(1)若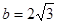 ,
, ,求△ABC的面积;
,求△ABC的面积;
(2)若 成等比数列,试判断△ABC的形状。
成等比数列,试判断△ABC的形状。
已知直线l1:x+my+6=0,l2:(m-2)x+3y+2m=0,
求m的值,使得:(1)l1⊥l2;(2) l1∥l2
在等差数列 中,
中, ,
, ,记数列
,记数列 的前
的前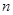 项和为
项和为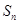 .
.
(1)求数列 的通项公式;
的通项公式;
(2)是否存在正整数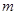 、
、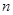 ,且
,且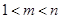 ,使得
,使得 、
、 、
、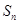 成等比数列?若存在,求出所有符合条件的
成等比数列?若存在,求出所有符合条件的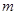 、
、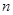 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.