某运输公司接受了向抗洪救灾地区每天送至少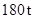 支援物资的任务.该公司有
支援物资的任务.该公司有 辆载重
辆载重 的
的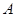 型卡车与
型卡车与 辆载重为
辆载重为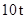 的
的 型卡车,有
型卡车,有 名驾驶员,每辆卡车每天往返的次数为
名驾驶员,每辆卡车每天往返的次数为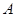 型卡车
型卡车 次,
次, 型卡车
型卡车 次;每辆卡车每天往返的成本费
次;每辆卡车每天往返的成本费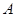 型为
型为 元,
元, 型为
型为 元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排
元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排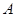 型或
型或 型卡车,所花的成本费分别是多少?
型卡车,所花的成本费分别是多少?
已知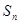 是等比数列{
是等比数列{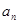 }的前
}的前 项和,
项和, 、
、 、
、 成等差数列.
成等差数列.
(Ⅰ)求数列{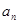 }的公比
}的公比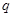 ;
;
(Ⅱ)求证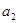 、
、 、
、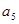 成等差数列.
成等差数列.
已知椭圆C的两焦点分别为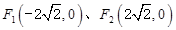 ,长轴长为6.
,长轴长为6.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知过点(0,2)且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度.
在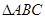 中,内角
中,内角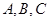 对边分别为
对边分别为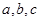 ,且
,且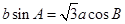 .
.
(Ⅰ)求角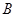 的大小;
的大小;
(Ⅱ)若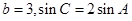 ,求
,求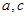 的值.
的值.
已知椭圆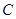 的中心为坐标原点O,焦点在
的中心为坐标原点O,焦点在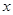 轴上,离心离为
轴上,离心离为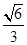 ,点B是椭圆短轴的下端点. B到椭圆一个焦点的距离为
,点B是椭圆短轴的下端点. B到椭圆一个焦点的距离为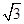 .
.
(Ⅰ)求椭圆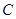 的方程;
的方程;
(Ⅱ)设过点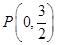 的直线
的直线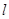 与椭圆
与椭圆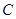 交于
交于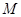 ,
,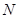 两点,且
两点,且 ,求直线
,求直线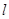 的方程.
的方程.
投资商到一开发区投资72万元建起一座蔬菜加工厂,经营中,第一年支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入50万元,设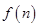 表示前n年的纯利润总和(
表示前n年的纯利润总和( 前
前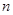 年总收入 前
年总收入 前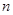 年的总支出 投资额72万元)
年的总支出 投资额72万元)
(Ⅰ)该厂从第几年开始盈利?
(Ⅱ)该厂第几年平均纯利润达到最大?并求出年平均纯利润的最大值.