如图所示,一传送带与水平面夹角为θ=30°,以2 m/s的恒定速度顺时针运行.现将一质量为10 kg的工件轻放于传送带底端,经一段时间送到高度为2 m的高处,工件与传送带间的动摩擦因数为μ=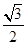 .求带动皮带的电动机由于传送工件多消耗的电能.
.求带动皮带的电动机由于传送工件多消耗的电能.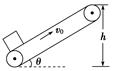
登山运动时,张捷用100min由宿营地X爬到山顶Y,在山道上通过的路程是2400m,相对于X升高了1200m,如图所示.
(1)由X到Y的位移是多少?
(2)爬山的平均速率是多大?
(3)计算他爬山的平均速度的大小?
光滑水平轨道上有三个木块A、B、C,质量分别为mA=3m、mB=mC=m,开始时B、C均静止,A以初速度νo向右运动,A与B相撞后分开,B又与C发生碰撞并粘在一起,此后A与B间的距离保持不变.求B与C碰撞前B的速度大小.
一个半圆柱形玻璃砖,其横截面是半径为R的半圆,AB为半圆的直径,O为圆心,如图所示,玻璃的折射率n= .
.
(i)一束平行光垂直射向玻璃砖的下表面,若光线到达上表面后,都能从该表面射出,则入射光束在AB上的最大宽度为多少?
(ii)一细束光线在O点左侧与O相距 R处垂直于AB从下方入射,求此光线从玻璃砖射出点的位置.
R处垂直于AB从下方入射,求此光线从玻璃砖射出点的位置.
如图所示,开口向上粗细均匀的玻璃管长L=l00cm,管内有一段高h=20cm的水银柱,封闭着长a=50cm的空气柱,大气压强P0=76cmHg,温度t0=27℃.求温度至少升到多高时,可使水银柱全部溢出?
一个质量为m带电量为q的小球,以初速度v0自离地面h高度处水平抛出.重力加速度为g,空气阻力忽略不计.
(1)求小球自抛出到第一次落地点P的过程中发生的水平位移x的大小.
(2)若在空间加一个竖直方向的匀强电场,发现小球以相同方式水平抛出后做匀速直线运动,请判断电场的方向并求出电场强度E的大小.
(3)若在空间再加一个垂直纸面的匀强磁场,发现小球以相同方式水平抛出后第一次落地点仍然是P.已知OP间的距离大于h,请判断磁场的方向并求出磁感应强度B的大小.