已知 ,求代数式
,求代数式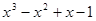 的值.
的值.
完成下面推理过程: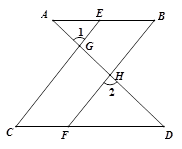
如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(_______________________),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________________).
∴∠=∠C(__________________________).
又∵∠B =∠C(已知),
∴∠=∠B(等量代换).
∴AB∥CD(________________________________).
如图,∠AOB内一点P:
(1)过点P画PC∥OB交OA于点C,画PD∥OA交OB于点D;
(2)写出两个图中与∠O互补的角;
(3)写出两个图中与∠O相等的角.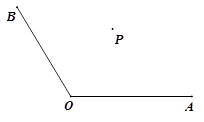
如图,在平面直角坐标系xOy中,二次函数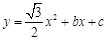 的图象与
的图象与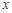 轴交于
轴交于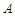 (-1,0)、
(-1,0)、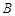 (3,0)两点, 顶点为
(3,0)两点, 顶点为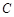 .
.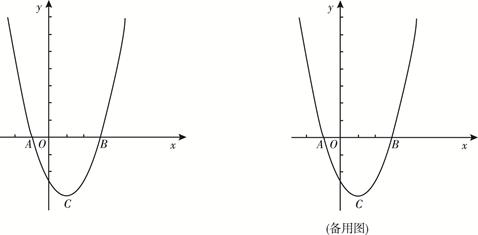
(1) 求此二次函数解析式;
(2) 点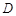 为点
为点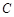 关于x轴的对称点,过点
关于x轴的对称点,过点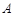 作直线
作直线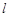 :
: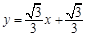 交BD于点E,过点
交BD于点E,过点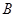 作直线
作直线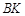 ∥
∥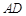 交直线
交直线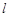 于
于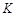 点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
(3) 在(2)的条件下,若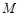 、
、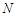 分别为直线
分别为直线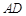 和直线
和直线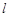 上的两个动点,连结
上的两个动点,连结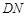 、
、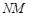 、
、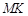 ,求
,求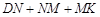 和的最小值.
和的最小值.
在Rt△ABC中,∠ACB=90°,tan∠BAC=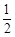 . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设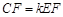 ,则k =;
,则k =;
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
已知,二次函数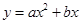 的图象如图所示.
的图象如图所示.
(1)若二次函数的对称轴方程为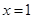 ,求二次函数的解析式;
,求二次函数的解析式;
(2)已知一次函数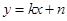 ,点
,点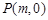 是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数
是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数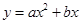 的图象于点N.若只有当1<m<
的图象于点N.若只有当1<m<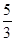 时,点M位于点N的上方,求这个一次函数的解析式;
时,点M位于点N的上方,求这个一次函数的解析式;
(3)若一元二次方程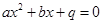 有实数根,请你构造恰当的函数,根据图象直接写出
有实数根,请你构造恰当的函数,根据图象直接写出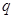 的最大值.
的最大值.