目前,包括长江、黄河等七大流域在内,全国水土流失面积达到367万平方千米,其中长江与黄河流域的水土流失总面积占全国的32.4%。而长江流域的水土流失问题更为严重,它的水土流失面积比黄河流域的水土流失面积还要多29万平方千米。问长江流域的水土流失面积是多少(结果保留整数)?
甲、乙两位同学本学年每个单元的测验成绩如下(单位:分):
甲:98,100,100,90,96,91,89,99,100,100,93
乙:98,99,96,94,95,92,92,98,96,99,97
(1)、他们的平均成绩分别是多少?
(2)、甲、乙的11次单元测验成绩的标准差分别是多少?
(3)、这两位同学的成绩各有什么特点?
(4)、现要从中选出一人参加“希望杯”竞赛,历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,你认为应选谁参加这项竞赛,为什么?
已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、C(2,3).请回答如下问题: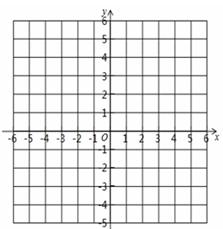
(1)在坐标系内描出点A、B、C的位置,并求△ABC的面积;
(2)在平面直角坐标系中画出△ ,使它与△ABC 关于x轴对称,并写出△
,使它与△ABC 关于x轴对称,并写出△ 三顶点的坐标.
三顶点的坐标.
(3)若M(x,y)是△ABC内部任意一点,请直接写出这点在△ 内部的对应点M'的坐标.
内部的对应点M'的坐标.
解方程组(1)、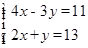 (2)、
(2)、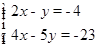
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(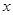 表示乌龟从起点出发所行的时间,表示乌龟所行的路程,
表示乌龟从起点出发所行的时间,表示乌龟所行的路程,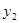 表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处追上乌龟.其中正确的说法是.(把你认为正确说法的序号都填上)
表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处追上乌龟.其中正确的说法是.(把你认为正确说法的序号都填上)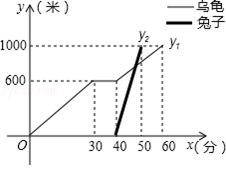
己知数轴甲上有A、B、C三点,分别表示-30、-20、0,动点P从点A山发,以每秒1个单位的速度向终点C移动,设点P移动的时间为t秒,点P在数轴甲上表示数P.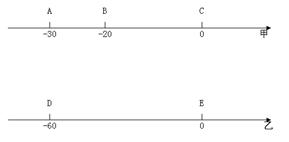
(1)用含t的代数式表示p.
(2)另有一个数轴乙,数轴乙上有D、E两点,分别表示-60、0,点D、E分别在数轴甲上的点A、C的正下方,当点P运动到点B时,数轴乙上的动点Q从点D出发,以点P速度的四倍向点E运动,点Q到达点E后,再立即以同样的速度返回,当点P到达点C时,P、Q两点运动停止,设点Q在数轴乙上表示数q.
①求当点Q从开始运动到运动停止时,p-q的值(用含t的代数式表示);
②求当t为何值时,p=q?