“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(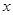 表示乌龟从起点出发所行的时间,表示乌龟所行的路程,
表示乌龟从起点出发所行的时间,表示乌龟所行的路程,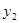 表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处追上乌龟.其中正确的说法是 .(把你认为正确说法的序号都填上)
表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处追上乌龟.其中正确的说法是 .(把你认为正确说法的序号都填上)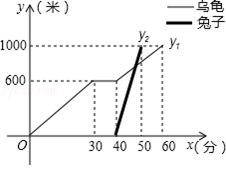
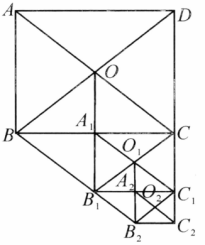
如图,在矩形 中, ,两条对角线相交于点 .以 为邻边作第 个平行四边形 ,对角线相交于点 ;再以 为邻边作第 个平行四边形 ,对角线相交于点 ;再以 为邻边作第 个平行四边形 ;…,依此类推.
(1)求矩形 的面积;
(2)求第 个平行四边形 、第 个平行四边形 和第 个平行四边形的面积.
如图, 分别是四边形 各边中点.
(1)若四边形 是任意四边形、则四边形 是怎样的四边形?
(2)若四边形 是矩形,则四边形 是怎样的四边形?
(3)若四边形 分別菱形、正方形、等腰梯形时,则四边形 又分别是怎样的四边形?
(4)若四边形 是矩形,则四边形 有什么特征?
(5)若四边形 分别是菱形、正方形时,则四边形 又有什么特征?

如图,正方形 的边长为 ,点 , , , 分别在正方形的四条边上,已知 , .
(1)若 ,求四边形 的周长和面积;
(2)求四边形 的周长的最小值.

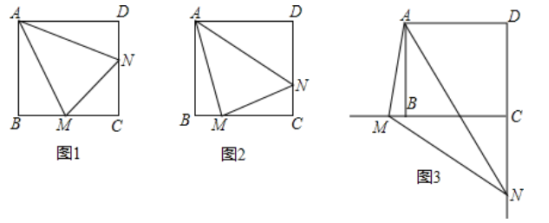
已知正方形 中, 绕点 顺时针旋转,它的两边分别交 (或它们的延长线)于点 .当 绕点 旋转得到 时(如图1),易证 .
(1)当 绕点 旋转到 时(如图2),线段 和 之间有怎样的数量关系?写出猜想,并加以证明;
(2)当 绕点 旋转到如图3的位置时,线段 和 之间又有怎样的数量关系?写出你的猜想,并说明理由.
如图,将边长为 的正方形 折叠,使得 点落在 上的 点,然后压平得折痕 ,若 ,求线段 之长.
