如图， 分别是四边形 各边中点.
（1）若四边形 是任意四边形、则四边形 是怎样的四边形?
（2）若四边形 是矩形，则四边形 是怎样的四边形?
（3）若四边形 分別菱形、正方形、等腰梯形时，则四边形 又分别是怎样的四边形?
（4）若四边形 是矩形，则四边形 有什么特征?
（5）若四边形 分别是菱形、正方形时，则四边形 又有什么特征?
先化简，再求值：
，其中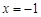
.
在Rt△ABC中，∠A=90°，AB=6，AC=8，点D为边BC的中点，DE⊥BC交边AC于点E，点P为射线AB上一动点，点Q为边AC上一动点，且∠PDQ=90°．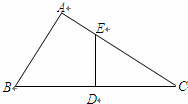 
（1）求ED、EC的长；
（2）若BP=2，求CQ的长；
（3）记线段PQ与线段DE的交点为点F，若△PDF为等腰三角形，求BP的长．
已知：直线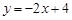
交x轴于点A，交y轴于点B，点C为x轴上一点，AC=1，且OC＜OA．抛物线
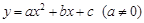经过点A、B、C．
（1）求该抛物线的表达式；
（2）点D的坐标为（-3，0），点P为线段AB上一点，当锐角∠PDO的正切值为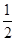
时，求点P的坐标；
（3）在（2）的条件下，该抛物线上的一点E在x轴下方，当△ADE的面积等于四边形APCE的面积时，求点E的坐标．
已知：如图，在正方形ABCD中，点E、F分别在边BC和CD上，∠BAE=∠DAF．
（1）求证：BE=DF；
（2）联结AC交EF于点O，延长OC至点M，使OM= OA，联结EM、FM．求证：四边形AEMF是菱形．
某超市进了一批成本为6元/个的文具．调查后发现：这种文具每周的销售量y（个）与销售价x（元/个）之间的关系满足一次函数关系，如下表所示：
| 销售价x（元/个） |
8 |
9.5 |
11 |
14 |
| 销售量y（个） |
220 |
205 |
190 |
160 |
（1）求y与x之间的函数解析式（不必写出定义域）；
（2）已知该超市这种文具每周的销售量不少于60个，若该超市某周销售这种文具（不考虑其它因素）的利润为800元，求该周每个文具的销售价．