统计表明,某种型号的汽车在匀速行驶中每小时的耗油量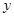 (升)关于行驶速度
(升)关于行驶速度 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
(本小题满分12分)
已知向量 ,
, ,函数
,函数 .
.
(1)求 的最大值及相应的
的最大值及相应的 的值;
的值;
(2)若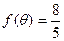 ,求
,求 的值.
的值.
(本小题满分12分)
某货轮在A处看灯塔B在货轮北偏东 ,距离为
,距离为 n mile;在A处看灯塔C在货轮的北偏西
n mile;在A处看灯塔C在货轮的北偏西 ,距离为
,距离为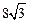 n mile.货轮由A处向正北航行到D处时,再看灯塔B在北偏东
n mile.货轮由A处向正北航行到D处时,再看灯塔B在北偏东 ,求:
,求:
(Ⅰ)A处与D处之间的距离;
(Ⅱ)灯塔C与D处之间的距离.
(本小题 满分12分)
满分12分)
已知等差数列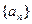 满足
满足
(1)求数列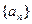 的通项公式;
的通项公式;
(2)设各项均为正数的等比数列 的前n项和为Tn若
的前n项和为Tn若 求
求
(本小题满分14分)
设数列 的通项公式为
的通项公式为 . 数列
. 数列 定义如下:对于正整数m,
定义如下:对于正整数m,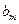 是使得不等式
是使得不等式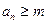 成立的所有n中的最小值.
成立的所有n中的最小值.
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)若 ,求数列
,求数列 的前2m项和公式;
的前2m项和公式;
(Ⅲ)是否存在p和q,使得 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
(本小题满分14分)
已知圆 方程为:
方程为: .
.
(Ⅰ)直线 过点
过点 ,且与圆
,且与圆 交于
交于 、
、 两点,若
两点,若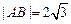 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)过圆 上一动点
上一动点 作平行于
作平行于 轴的直线
轴的直线 ,设
,设 与
与 轴的交点为
轴的交点为 ,若向量
,若向量 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.