将一个长方形绕它的一边所在的直线旋转一周，得到的几何体是圆柱，现有一个长为4cm、宽为3cm的长方形，分别绕它的长、宽所在的直线旋转一周，得到的圆柱体的体积分别是多少？（友情提示：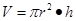
，其中
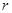代表圆柱底面半径，
代表圆柱高）（结果保留
）
（1）如图1是一个重要公式的几何解释．请你写出这个公式；
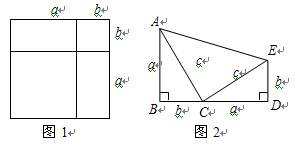
（2）如图2，
，
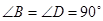，且
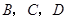三点共线．
试证明
；
M是大于负50的立方根的最小整数,N是小于50的平方根的最大整数,求M加N的平方根，
已知，如图，点B、F、C、E在同一直线上，AC、DF相交于点G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AB＝DE，BF＝CE。求证：（1）△ABC≌△DEF；（2）GF＝GC。
（1）计算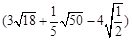
÷
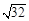；（2）分解因式
．
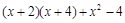在平面直角坐标系
中,已知二次函数
的图象经过点
和点
,直线
经过抛物线的顶点且与
轴垂直,垂足为
.求该二次函数的表达式；
设抛物线上有一动点
从点
处出发沿抛物线向上运动,其纵坐标
随时间
≥
)的变化规律为
.现以线段
为直径作
.
①当点在起始位置点处时,试判断直线与的位置关系,并说明理由；在点运动的过程中,直线与是否始终保持这种位置关系? 请说明你的理由；
②若在点开始运动的同时,直线也向上平行移动,且垂足的纵坐标
随时间
的变化规律为
,则当在什么范围内变化时,直线与相交? 此时,若直线被所截得的弦长为
,试求
的最大值.