如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB 所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2=" 17," 且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.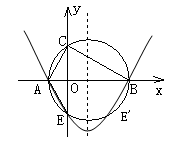
(1)求C点的坐标;
(2)以斜边AB为直径作圆与y轴交于另一点E,求过A、B、E 三点的抛物线的关系式,并画出此抛物线的草图.
(3)在抛物线上是否存在点P,使△ABP与△ABC全等?若存在,求出符合条件的P点的坐标;若不存在,说明理由.
某商场销售一批名牌服装,平均每天可售出20件,每件盈利40元,为了增加盈利,商场决定采取适当的降价措施,经调查发现.如果每件服装每降低1元,商场平均每天可多售出2件.若商场平均每天要盈利1200元,问每件服装应降价多少元?
如图,AB为⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠DCB=∠A.求证:CD是⊙O的切线.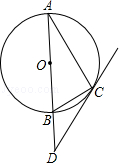
袋中有大小相同的红球和白球共5个,任意摸出一红球的概率是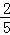 .求:
.求:
(1)袋中红球、白球各有几个?
(2)任意摸出两个球(不放回)均为红球的概率是多少?
如图,△ABC中,∠B=10°,∠ACB=20°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.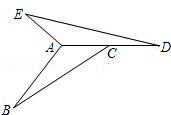
(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
解下列方程:(1)x2﹣4x﹣7=0(2)(2x﹣1)2=(3﹣x)2.