袋中有大小相同的红球和白球共5个,任意摸出一红球的概率是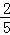 .求:
.求:
(1)袋中红球、白球各有几个?
(2)任意摸出两个球(不放回)均为红球的概率是多少?
如图,在菱形 中,点 是边 上一点,延长 至点 ,使 ,连接 、 .
求证: .

2016年4月23日是我国第一个"全民阅读日".某校开展了"建设书香校园,捐赠有益图书"活动.我们在参加活动的所有班级中,随机抽取了一个班,已知这个班是八年级5班,全班共50名学生.现将该班捐赠图书的统计结果,绘制成如下两幅不完整的统计图.

请你根据以上信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)求八年级5班平均每人捐赠了多少本书?
(3)若该校八年级共有800名学生,请你估算这个年级学生共可捐赠多少本书?
如图,已知锐角 ,点 是 边上的一定点,请用尺规在 边上求作一点 ,使 与 相似.(作出符合题意的一个点即可,保留作图痕迹,不写作法.

特例感知
(1)如图1,对于抛物线 , , ,下列结论正确的序号是 ;
①抛物线 , , 都经过点 ;
②抛物线 , 的对称轴由抛物线 的对称轴依次向左平移 个单位得到;
③抛物线 , , 与直线 的交点中,相邻两点之间的距离相等.
形成概念
(2)把满足 为正整数)的抛物线称为“系列平移抛物线”.
知识应用
在(2)中,如图2.
①“系列平移抛物线”的顶点依次为 , , , , ,用含 的代数式表示顶点 的坐标,并写出该顶点纵坐标 与横坐标 之间的关系式;
②“系列平移抛物线”存在“系列整数点(横、纵坐标均为整数的点)”: , , , , ,其横坐标分别为 , , , , 为正整数),判断相邻两点之间的距离是否都相等,若相等,直接写出相邻两点之间的距离;若不相等,说明理由.
③在②中,直线 分别交“系列平移抛物线”于点 , , , , ,连接 , ,判断 , 是否平行?并说明理由.

在图1,2,3中,已知 , ,点 为线段 上的动点,连接 ,以 为边向上作菱形 ,且 .

(1)如图1,当点 与点 重合时, ;
(2)如图2,连接 .
①填空: (填“ ”,“ “,“ ” ;
②求证:点 在 的平分线上;
(3)如图3,连接 , ,并延长 交 的延长线于点 ,当四边形 是平行四边形时,求 的值.