已知等差数列{an}的首项a1=1,公差d>0,且第二项,第五项,第十四项分别是等比数列{bn}的第二项,第三项,第四项.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对任意自然数n,均有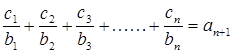 ,
,
求通项公式Cn 及c1+c2+c3+……+c2006值
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a. 
(1)求证:平面SAB⊥平面SAD;
(2)设SB的中点为M,当 为何值时,能使DM⊥MC?请给出证明.
为何值时,能使DM⊥MC?请给出证明.
已知正四棱柱ABCD-A1B1C1D1,AB=1,AA1=2,点E为CC1中点,点F为BD1中点. 
(1)证明:EF为BD1与CC1的公垂线(即证EF与BD1、CC1都垂直);
(2)求点D1到面BDE的距离.
已知ABCD是梯形,AD∥BC,P是平面ABCD外一点,
BC=2AD,点E在棱PA上,且PE=2EA.
求证:PC∥平面EBD.
.甲、乙两同学利用暑假到某县进行社会实践,对该县的养鸡场连续六年来的规模进行调查研究,得到如下两个不同的信息图.(A)图表明:从第1年平均每个养鸡场出产1万只鸡上升到第6年平均每个养鸡场出产2万只鸡;(B)图表明:由第1年养鸡场个数30个减少到第6年的10个.
请你根据提供的信息解答下列问题:
(1)第二年的养鸡场的个数及全县出产鸡的总只数各是多少?
(2)哪一年的规模最大?为什么?
已知数列{an}是等差数列,bn= ,b1+b2+b3=
,b1+b2+b3= ,b1b2b3=
,b1b2b3= ,求an.
,求an.