设集合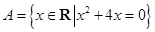 ,
,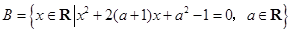 ,若
,若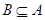 ,求实数
,求实数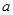 的值.
的值.
(本小题满分10分)已知函数
(1)若直线 与曲线
与曲线 相切,求实数
相切,求实数 的值;
的值;
(2)若 ,比较
,比较 与
与 的大小
的大小
(本小题满分12分)在锐角 中,已知内角
中,已知内角 、
、 、
、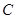 所对的边分别为
所对的边分别为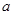 、
、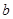 、
、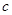 ,向量
,向量 ,且向量
,且向量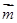 ,
, 共线.
共线.
(1)求角 的大小;
的大小;
(2)如果 ,求
,求 的面积
的面积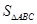 的最大值.
的最大值.
(本小题满分12分)已知函数 ,
,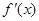 是
是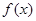 的导函数.
的导函数.
(1)求函数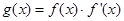 的最小值及相应的
的最小值及相应的 值的集合;
值的集合;
(2)若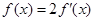 ,求
,求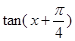 的值.
的值.
(本题10分)已知函数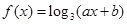 的图象经过点
的图象经过点 和
和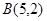 ,记
,记
(1)求数列 的通项公式;
的通项公式;
(2)设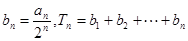 ,若
,若 ,求
,求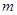 的最小值;
的最小值;
(3)求使不等式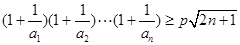 对一切
对一切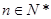 均成立的最大实数
均成立的最大实数 .
.
(本题8分)已知抛物线C: 和直线L:y =-2,直线L与y轴的交点D(0,-2),过点Q(0,2)的直线交抛物线C于A、B两点,与直线L交于点P.
和直线L:y =-2,直线L与y轴的交点D(0,-2),过点Q(0,2)的直线交抛物线C于A、B两点,与直线L交于点P.
(1)记 的面积为S,求S的取值范围;
的面积为S,求S的取值范围;
(2)设 ,
, ,求
,求 的值。
的值。