如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的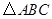 是格点三角形.在建立平面直角坐标系后,点
是格点三角形.在建立平面直角坐标系后,点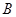 的坐标为(
的坐标为(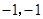 ).
).
(1)把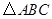 向左平移8格后得到
向左平移8格后得到 ,画出
,画出 的图形并写出点
的图形并写出点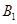 的坐标;
的坐标;
(2)把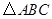 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转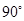 后得到
后得到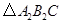 ,画出
,画出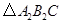 的图形并写出点
的图形并写出点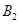 的坐标;
的坐标;
(3)把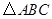 以点
以点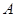 为位似中心放大,使放大前后对应边长的比为
为位似中心放大,使放大前后对应边长的比为 ,画出
,画出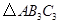 的图形.
的图形.
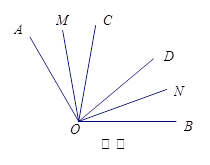
已知 ,
,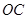 、
、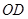 是过点
是过点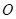 的射线,射线
的射线,射线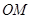 、
、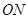 分别平分
分别平分 和
和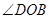 .
.
(1)如图①,若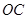 、
、 是
是 的三等分线,则
的三等分线,则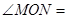 °
°
(2)如图②,若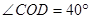 ,
,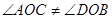 ,则
,则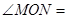 °
°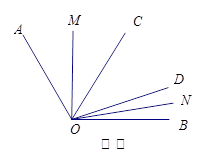
(3)如图③,在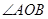 内,若
内,若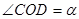 (
(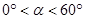 ),则
),则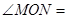 °
°
(4)将(3)中的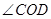 绕着点
绕着点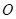 逆时针旋转到
逆时针旋转到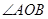 的外部(
的外部(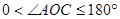 ,
,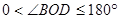 ),求此时
),求此时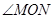 的度数.
的度数. 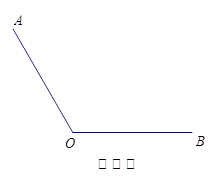
某体育文化用品店排球和篮球的进价和售价如下表1所示:

表1表2
①若该商店篮球打 折出售,则出售一个篮球,商店的利润为元;
折出售,则出售一个篮球,商店的利润为元;
若该商店排球打 折出售,则出售
折出售,则出售 个排球,商店的利润为元.
个排球,商店的利润为元.
②(列方程求解)为提高销量,该商店按表2中的优惠方式进行促销,现有一中学购买了篮球和排球共50个(篮球和排球数量不等),商店恰好获利305元,求该中学购买了篮球、排球各多少个?
如图,有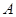 、
、 、
、 、
、 四个点,根据以下要求画图(保留画图痕迹)
四个点,根据以下要求画图(保留画图痕迹)
(1)画直线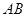 ;(2)画线段
;(2)画线段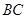 ;(3)画射线
;(3)画射线 ;
;
(4)若点 在点
在点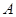 正东方向,那么点
正东方向,那么点 在点
在点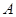 的方向;
的方向;
(5)在射线 上取线段
上取线段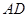 ,使
,使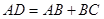 (尺规作图);
(尺规作图);
(6)在平面上确定一点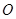 ,使
,使 的长度最短,这是根据原理.
的长度最短,这是根据原理.
列方程解应用题:
把一些苹果分给若干名学生,如果每人分10个,则剩余6个苹果;如果每人分12个苹果,则还少6个苹果.求共有多少学生?有多少个苹果?
先化简,再求值: ,
,
其中 是2的倒数,
是2的倒数, 是3的相反数.
是3的相反数.