(本小题满分14分)
已知抛物线方程为 ,在y轴上截距为2的直线l与抛物线交于M、N两点,O为坐标原点,若OM⊥ON,求直线l的方程.
,在y轴上截距为2的直线l与抛物线交于M、N两点,O为坐标原点,若OM⊥ON,求直线l的方程.
.(本小题满分12分)
设 是方程x2-ax+b=0的两个实根,试分析a>2且b>1是两根
是方程x2-ax+b=0的两个实根,试分析a>2且b>1是两根 均大于1的什么条件?说明理由.
均大于1的什么条件?说明理由.
(本小题10分)
设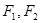 分别为椭圆
分别为椭圆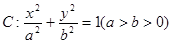 的左、右两个焦点.(1)若椭圆
的左、右两个焦点.(1)若椭圆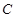 上的点
上的点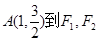 两点的距离之和等于4,求椭圆
两点的距离之和等于4,求椭圆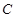 的方程和焦点坐标;(2)设点P是(1)中所得椭圆上的动点,
的方程和焦点坐标;(2)设点P是(1)中所得椭圆上的动点, 。
。
(本小题10分)
已知双曲线中心在原点,且一个焦点为F(,0),直线y=x-1与其相交于M、N两点,MN中点的横坐标为-,求此双曲线的方程.
(本小题10分)
设命题 :对任意实数x,不等式
:对任意实数x,不等式 恒成立;命题
恒成立;命题 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线.(1)若命题
轴上的双曲线.(1)若命题 为真命题,求实数
为真命题,求实数 的取值范围;(2)若命题:
的取值范围;(2)若命题:  为真命题,且“
为真命题,且“ ”为假命题,求实数m的取值范围.
”为假命题,求实数m的取值范围.