阅读理解题（本题共14分）
如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负。如果从A到B记为：A→B（＋1，＋4），从B到A记为：A→B（－1，－4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中
（1）A→C（ ， ），B→C（ ， ）,C→ （＋2， ）；
（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；
（3）若这只甲虫从A处去甲虫P处的行走路线依次为（＋2，＋2），（＋2，－1），（－2，＋3），（－1，－2），请在图中标出P的位置。
（4）请你为这只甲壳虫设计一种从A处去往E处的路线。
如图1，已知l1∥l2，MN分别和直线l1、l2交于点A、B，ME分别和直线l1、l2交于点C、D．点P在MN上（P点与A、B、M三点不重合）．∠PDB=α，∠PCA=β，∠CPD=γ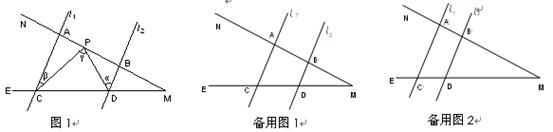
（1）如果点P在A、B两点之间运动时α、β、γ之间有何数量关系？请说明理由．
（2）如果点P在A、B两点外侧运动时α、β、γ之间有何数量关系？请说明理由．
已知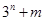
能被13整除,求证
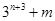也能被13整除、
①已知
求
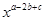的值。
②若n满足(n-2010)2+(2011-n)2=3，求(n-2010)(2011-n)的值。
③已知：多项式
中不含xy项．
求: 
的值、
观察下列各式：（x-1）(x+1)=x
–1
(x-1)(x+x+1)=x
-1
(x-1)(x+x+x+1)=x
-1
(x-1)(x+x+x+x+1)=x
-1
(1) 根据前面各式的规律可得：（x-1）(x
+x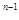
+…+x+1)= 、(其中n为正整数)
（2）根据（1）求：1+2+2+2+…+2
+2
的值，并求出它的个位数字。
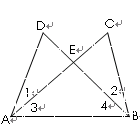
如图，给出下列论断：① DE= CE②∠1=∠2③∠3=∠4请你将其中的两个作为条件，另一个作为能成立的结论，并加以说明。（完成一种情况即可）