实践与探索:
㈠小明在玩积木游戏时,把三个正方形积木摆成一定的形状,正视图如图①,
问题(2):若P的面积为36cm2,Q的面积为64 cm2,同时M的面积为100 cm2,则△DEF为_______三角形。
㈡图形变化:Ⅰ.如图②,分别以直角三角形的三边为直径向三角形外作三个半圆,你能找出这三个半圆的面积之间有什么关系吗?请说明理由。
Ⅱ.如图③,如果直角三角形两直角边的长分别为3和4,以直角三角形的三边为直径作半圆,你能利用上面中的结论求出阴影部分的面积吗? 

已知抛物线y=ax2-2ax+c与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且OC=3OA.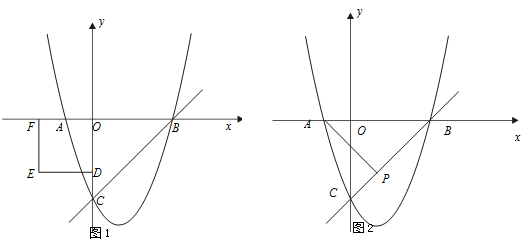
(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式;
②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
已知直线l经过正方形ABCD的顶点A,过点C作CE垂直直线l于点E,连接BE
(1)如图1,CE+AE=______BE,并说明理由.
(2)如图2,将直线l绕着点A,逆时针旋转到如图位置时,请判断(1)的结论是否成立,若成立请证明;若不成立,写出你认为正确的结论,并说明理由.
(3)如图3,将直线l绕着A,逆时针旋转到如图位置时,请直接写出线段BE、AE、CE三者数量关系,不必证明。
某商店购进一批单价为40元的纪念品,如果按每件50元出售,那么每天可销售200件,经市场调研发现,纪念品的销售单价每上涨1元,其销售量每天减少5件,如果每件纪念品的利润不超过50%,设纪念品的销售单价上涨x元,每天所获利润为y元.
(1)求y与x之间的函数关系式.
(2)将纪念品销售单价定为多少,才能使每天所获销售利润最大?最大利润是多少?
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点F.
(1)判断AF与⊙O的位置关系,并说明理由.
(2)若OC=CF,AB=12,求CD的长.
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
(1)m=,a =;
(2)求出甲车行驶路程y(km)与时间x(h)的函数解析式,并写出相应的x的取值范围;
(3)当乙车行驶多长时间时,两车恰好相距50km.