(本小题满分13分)如图(甲),在直角梯形ABED中,AB//DE,AB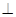 BE,AB
BE,AB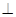 CD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点,现将△ACD沿CD折起,使平面ACD
CD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点,现将△ACD沿CD折起,使平面ACD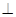 平面CBED,如图(乙).
平面CBED,如图(乙).
(1)求证:平面FHG//平面ABE;
(2)记
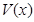 表示三棱锥B-ACE 的体积,求
表示三棱锥B-ACE 的体积,求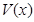 的最大值;
的最大值;
(3)当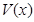 取得最大值时,求二面角D-AB-C的余弦值.
取得最大值时,求二面角D-AB-C的余弦值.
已知正项数列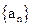 满足
满足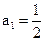 ,且
,且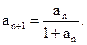
(1)求正项数列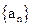 的通项公式;
的通项公式;
(2)求和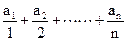
(1)设{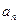 }是等差数列,求证:数列{
}是等差数列,求证:数列{ }是等差数列.
}是等差数列.
(2)在等差数列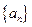 中,
中, 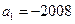 ,其前
,其前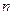 项的和为
项的和为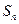 ,若
,若 ,求
,求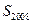 .
.
求出下列等差数列中的未知项:
(1)m, 3, 5, n;
(2)3, m , n, -9, p, q.
如下图所示是一个计算机程序运行装置示意图, 是数据入口,C是计算结果出口,计算过程是:由
是数据入口,C是计算结果出口,计算过程是:由 分别输入正整数m和n,经过计算后得出的正整数k由C输出。此种计算装置完成的计算满足:①若
分别输入正整数m和n,经过计算后得出的正整数k由C输出。此种计算装置完成的计算满足:①若 分别输入1,则输出结果为1;②若
分别输入1,则输出结果为1;②若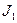 输入任意固定的正整数,
输入任意固定的正整数, 输入的正整数增加1,则输出的结果比原来增加2;③若
输入的正整数增加1,则输出的结果比原来增加2;③若 输入1,
输入1,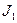 输入的正整数增加1,则输出结果为原来的2倍,试问:
输入的正整数增加1,则输出结果为原来的2倍,试问:
(1)若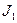 输入1,
输入1, 输入正整数n,输出结果为多少?
输入正整数n,输出结果为多少?
(2)若 输入1,
输入1,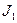 输入正整数m,输出结果为多少?
输入正整数m,输出结果为多少?
(3)若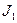 输入正整数m,
输入正整数m, 输入正整数n,输出结果为多少?
输入正整数n,输出结果为多少?
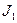 m n
m n
已知关于x的二次方程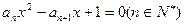 的两根
的两根 满足
满足 ,且
,且
(1)试用 表示
表示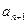 (2)求证:
(2)求证: 是等比数列
是等比数列
(3)求数列的通项公式 (4)求数列
(4)求数列 的前n项和
的前n项和