(本小题满分14分)
已知函数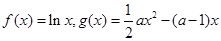 ,(
,(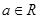 ).
).
(Ⅰ)已知函数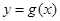 的零点至少有一个在原点右侧,求实数
的零点至少有一个在原点右侧,求实数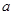 的范围.
的范围.
(Ⅱ)记函数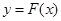 的图象为曲线
的图象为曲线 .设点
.设点 ,
,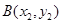 是曲线
是曲线 上的不同两点.如果在曲线
上的不同两点.如果在曲线 上存在点
上存在点 ,使得:①
,使得:① ;②曲线
;②曲线 在点
在点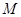 处的切线平行于直线
处的切线平行于直线 ,则称函数
,则称函数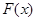 存在“中值相依切线”.
存在“中值相依切线”.
试问:函数 (
(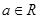 且
且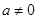 )是否存在“中值相依切线”,请说明理由.
)是否存在“中值相依切线”,请说明理由.
(本小题满分12分)
已知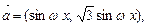



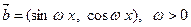 ,
,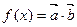 ,
,
且 的最小正周期为
的最小正周期为 .
.
(1)求 的单调递减区间. (2)求
的单调递减区间. (2)求 在区间
在区间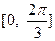 上的取值范围.
上的取值范围.
(本小题12分)做投掷2颗骰子的试验,用(x,y)表示结果,其中x表示第1颗骰子出现的点数,y 表示第2颗骰子出现的点数,写出:
(1)求事件“出现点数相等”的概率(2)求事件“出现点数之和大于8”的概率。
(本小题12分)某射手在一次射击训练中,射中10环,9环,8环、7环的概率分别是0.21,0.23,0.25,0.28,计算这个射手在一次射击中:
(1)射中10环或7环的概率;(2)不够7环的概率。
(本小题12分) 在平面直角坐标系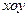 中,点A(-1,-2)、B(2,3)、C(-2,-1)。
中,点A(-1,-2)、B(2,3)、C(-2,-1)。
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足( )·
)·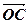 =0,求t的值。
=0,求t的值。
(本小题满分15分)已知 是定义在
是定义在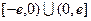 上的奇函数,当
上的奇函数,当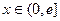 时,
时,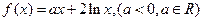
(1)求 的解析式;
的解析式;
(2)是否存在实数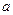 ,使得当
,使得当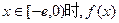 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出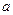 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。