(本小题满分12分)
设A1、A2是双曲线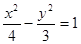 的实轴两个端点,P1P2是双曲线的垂直于
的实轴两个端点,P1P2是双曲线的垂直于 轴的弦,
轴的弦,
(Ⅰ)直线A1P1与A2P2交点P的轨迹 的方程;
的方程;
(Ⅱ)过 与
与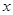 轴的交点Q作直线与(1)中轨迹
轴的交点Q作直线与(1)中轨迹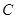 交于M、N两点,连接FN、FM,其中F
交于M、N两点,连接FN、FM,其中F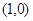 ,求证:
,求证: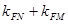 为定值;
为定值;
设f(x)=3ax2+2bx+c,若a+b+c=0,f(0)>0,f(1)>0
求证:(1)a>0,-2< <-1
<-1
(2)函数f(x)在(0,1)内有零点。
若a2-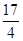 a+1<0,求使不等式x2+ax+1>2x+a成立的x的取值范围.
a+1<0,求使不等式x2+ax+1>2x+a成立的x的取值范围.
(本小题共14分)
已知椭圆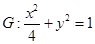 .过点(m,0)作圆
.过点(m,0)作圆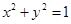 的切线I交椭圆G于A,B两点.
的切线I交椭圆G于A,B两点.
(I)求椭圆G的焦点坐标和离心率;
(II)将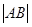 表示为m的函数,并求
表示为m的函数,并求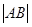 的最大值.
的最大值.
(本小题满分13分)双曲线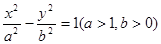 的焦距为2c,直线
的焦距为2c,直线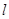 过点(a,0)和(0,b),且点(1,0)到直线
过点(a,0)和(0,b),且点(1,0)到直线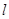 的距离与点(-1,0)到直线
的距离与点(-1,0)到直线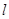 的距离之和
的距离之和 求双曲线的离心率e的取值范围.
求双曲线的离心率e的取值范围.
(本小题满分14分)
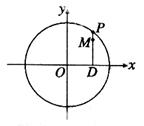
如图,设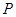 是圆
是圆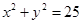 上的动点,点D是
上的动点,点D是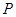 在
在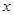 轴上的投影,M为
轴上的投影,M为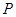 D上一点,且
D上一点,且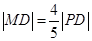
(Ⅰ)当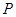 的在圆上运动时,求点M的轨迹C的方程;
的在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为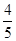 的直线被C所截线段的长度。
的直线被C所截线段的长度。