如图，在直角梯形ABCD中，AB∥DC，AB⊥BC，∠A=60°，AB=2CD，E、F分别为AB、AD的中点，联结EF、EC、BF、CF．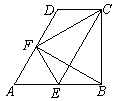
（1）四边形AECD的形状是 ；
（2）若CD=2，求CF的长．
①如图：A、B是两个蓄水池，都在河流a的同侧，为了方便灌溉作物，要在河边建一个抽水站， 将河水送到A、B两地，问该站建在河边什么地方，可使所修的渠道最短，试在 图中确定该点（保留作图痕迹）
②如图：某地有两所大学M、N和两条相交叉的公路a、b，现计划修建一座物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等。你能确定仓库应该建在什么位置吗？在所给的图形中画出你的设计方案；
如图，点E、F在BC上，BE=FC，AB=DC，∠B=∠C．求证：∠A=∠D．
如下图，一个点从数轴上的原点开始，先向右移动了3个单位长度，再向左移动5个单位长度，可以看到终点表示的数是-2，已知点A、B是数轴上的点，完成下列各题：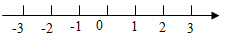
（1）如果点A表示数-3，将点A向右移动7个单位长度，那么终点B表示的数是_________，A、B两点间的距离是________．
（2）如果点A表示数是3，将点A向左移动7个单位长度，再向右移动5个单位长度，那么终点B表示的数是_______，A、B两点间的距离是________。一般地，如果点A表示数为a，将点A向右移动b个单位长度，再向左移动c个单位长度，那么请你猜想终点B表示的数是________，A、B两点间的距离是______．
观察下列等式：
，
，
，将以上三个等式相加得：
1－
＋－
＋－
＝1－＝
。
（1）猜想并写出：
＝．
（2）直接写出结果：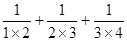
＋…＋
．
．有理数a、b所表示的点在数轴上的位置如图所示，请在数轴上标出它们的相反数，并将这四个数及0按从小到大的顺序用“<”连接起来.