如图1，抛物线y＝nx2－11nx＋24n (n＜0) 与x轴交于B、C两点（点B在点C的左侧），抛物线上另有一点A在第一象限内，且∠BAC＝90°．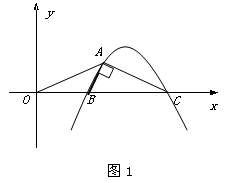
（1）填空：点B的坐标为（_ ），点C的坐标为（_ ）；
（2）连接OA，若△OAC为等腰三角形．
①求此时抛物线的解析式；
②如图2，将△OAC沿x轴翻折后得△ODC，点M为①中所求的抛物线上点A与点C两点之间一动点，且点M的横坐标为m，过动点M作垂直于x轴的直线l与CD交于点N，试探究：当m为何值时，四边形AMCN的面积取得最大值，并求出这个最大值．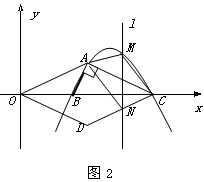
佛山市客运管理部门对“十一”国庆假期七天的客流变化量进行了不完全统计，
数据如下表（用正数表示客流量比前一天上升数，用负数表示下降数）：
| 日期 |
1日 |
2日 |
3日 |
4日 |
5日 |
6日 |
7日 |
| 变化/万人 |
10 |
-3 |
-5 |
-1 |
2 |
5 |
3 |
（1）国庆期间，10月_____日的客流量最低；（直接写出日期）
（2）与9月30日相比，10月7日的客流量是上升了还是下降了？变化了多少？
矿井下A，B，C三处的高度分别是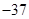
，
，
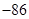
，A处比B处高多少米？C处比B处低多少米？
如题20图是由几个小正方体堆成的几何体，请在所给的网格图中分别画出从正面、
从上面看到这个几何体的形状图．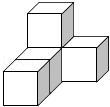
在数轴上将下列各数表示出来，并比较各数的大小，用“>”号连接起来．
，0，
，
，
，
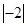（本题6分）如图1是用硬纸板做成的两个全等的直角三角形，两直角边的长分别为a和b，斜边长为c，如图2是以c为直角边的等腰直角三角形．请你开动脑筋，将它们拼成一个能证明勾股定理的图形．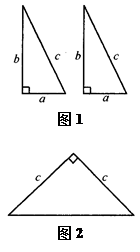
（1）画出拼成的这个图形的示意图；
（2）用这个图形证明勾股定理；
（3）假设图1中的直角三角形有若干个，你能只运用图1中所给的直角三角形拼出另一种能证明勾股定理的图形吗？请画出拼后的示意图（无需证明）．