已知 为空间四边形
为空间四边形 的边
的边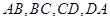 上的点,且
上的点,且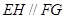 ,求证:
,求证:
本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元。甲、乙电视台的广告收费标准分别为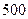 元/分钟和200元/分钟。假定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元。问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟。假定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元。问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
14分)某地计划从2006年起,用10年的时间创建50所“标准化学校”,已知该地在2006年投入经费为a万元,为保证计划的顺利落实,计划每年投入的经费都比上一年增加50万元。
(1)求该地第n年的经费投入y(万元)与n(年)的函数关系式;
(2)若该地此项计划的总投入为7250万元,则该地在2006年投入的经费a等于多少?
在△ABC中,已知,a= ,
,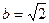 ,B=450求A、C及c
,B=450求A、C及c
已知 的前项之和
的前项之和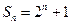 ,求此数列的通项公式。
,求此数列的通项公式。
设数列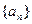 前n项和为Sn,且
前n项和为Sn,且 (Ⅰ)求
(Ⅰ)求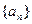 的通项公式;
的通项公式;
(Ⅱ)若数列{bn}满足b1=1且bn+1=bn+an(n≥1),求数列{bn}的通项公式