已知，如图抛物线y＝ax2＋3ax＋c(a>0)与y轴交于C点，与x轴交于A、B两点，A点在B点左侧．点B的坐标为(1,0)，OC＝3OB.
(1)求抛物线的解析式；
(2)若点D是线段AC下方抛物线上的动点，求四边形ABCD的面积的最大值；
(3)若点E在x轴上，点P在抛物线上，是否存在以A、C、E、P为顶点且以AC为一边的平行四边形？若存在，求点P的坐标；若不存在，请说明理由．
已知：抛物线
经过B（3，0）、C（0，3）两点，顶点为A．
求：（1）抛物线的表达式；
（2）顶点A的坐标．
在下面直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a、b、c满足关系式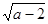
+（b-3）2=0，（c-4）2≤0.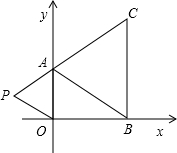
（1）求a、b、c的值；
（2）如果在第二象限内有一点P（m，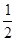
），请用含m的式子表示四边形ABOP的面积；
（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标，若不存在，请说明理由．
如图，已知EF∥CD，∠A=110°，∠EFC=35°，CF为∠ACD的平分线，那么AB与CD平行吗？说明理由.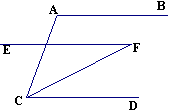
如图，直线AB、CD相交于点O，OE⊥AB，且∠DOE=4∠COE，求∠AOD的度数.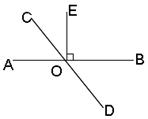
请在右图中，建立一个平面直角坐标系，使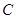
、
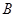的坐标分别为(0，1)和(5，
)，
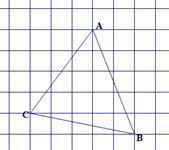
（1）写出点
的坐标；
（2）求三角形ABC的面积．