如图所示,质量为m的物体在倾角为α的斜面上,物体与斜面间的动摩擦因数为μ,如沿水平方向加一个力F,使物体以加速度a沿斜面向上做匀加速直线运动,则F的大小是多少?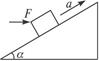
国内最长的梅溪湖激光音乐喷泉,采用了世界一流的喷泉、灯光和音响设备,呈现出让人震撼的光与水的万千变化,喷泉的水池中某一彩灯发出的一条光线射到水面的入射角为 ,从水面上射出时的折射角是
,从水面上射出时的折射角是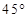 。
。
①求光在水面上发生全反射的临界角;
②在水池中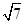 m深处有一彩灯(看做点光源)。求这盏彩灯照亮的水面面积。
m深处有一彩灯(看做点光源)。求这盏彩灯照亮的水面面积。
有一种方便旅游时携带的运动水壶,它可以充分压缩、折叠。甲图是它的实物图。乙图是它的使用原理图。需要使用的时候,首先将其向水壶口一边推动,形成一个类半圆形物体,然后再拉动水壶底部拉环,把另一个藏起来的半圆往外拽。这样,压缩的水壶就充分膨胀起来,可以装载液体了;这款伸缩水壶在旅行时携带十分方便,能减轻不少行李的压力。如果此水壶的容积为2L,在通过拉环使其膨起过程中,里面充入1.0atm 的1.6L空气时,将水壶口拧紧。求:
①水壶内部的气体分子数;
②当拉环完全拉开,水壶恢复正常形状时,内部空气的压强多大。
如图所示,滑块的质量m1="0.1" kg,用长为L的细线悬挂质量为m2="0.1" kg的小球,小球可视为质点,滑块与水平地面间及滑块与传送带间的动摩擦因数均为μ=0.2,滑块到小球及小球到传送带的距离均为s="2" m,传送带以v=4m/s的恒定速度匀速逆时针转动,传送带足够长。开始时,滑块以速度v0="8" m/s沿水平方向向右运动,并与小球发生弹性正碰,碰后小球能在竖直平面内做完整的圆周运动。问: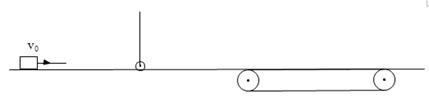
(1)细线长度L应该满足什么条件?
(2)若碰撞后小球恰能在竖直平面内完成完整的圆周运动并再次与滑块弹性正碰,则滑块与小球第一次碰撞后瞬间,悬线对小球的拉力多大?
(3)滑块从滑上传送带到从传送带上滑下,一共产生多少热量?(重力加速度g=10m/s2)
在直角坐标系xoy中,有一半径为R的圆形磁场区域,磁感强度为B,磁场方向垂直于xoy平面指向纸面外,该区域的圆心坐标为(0,R),P1 P2分别为加速电场的正负两极板,P2中央有一小孔,两极板平行于都x轴正对放置,如图所示。有一个质量为m电量为q的负离子,由静止经电场加速后从点( ,0)沿y轴正向射入第I象限,不计重力的影响。
,0)沿y轴正向射入第I象限,不计重力的影响。
(1)若离子从射入到射出磁场通过了该磁场的最大距离,试求离子在磁场区域经历的时间t1和加速电场的加速电压U1
(2)若离子在磁场区域经历的时间 ,求加速电场的加速电压U2.
,求加速电场的加速电压U2.
如图所示,在xOy平面内存在I、II、III、IV四个场区,y轴右侧存在匀强磁场I,y轴左侧与虚线MN之间存在方向相反的两个匀强电场,II区电场方向竖直向下,III区电场方向竖直向上,P点是MN与x轴的交点。有一质量为m,带电荷量+q的带电粒子由原点O,以速度v0沿x轴正方向水平射入磁场I,已知匀强磁场I的磁感应强度垂直纸面向里,大小为B0,匀强电场II和匀强电场III的电场强度大小均为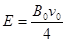 ,如图所示,IV区的磁场垂直纸面向外,大小为
,如图所示,IV区的磁场垂直纸面向外,大小为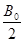 ,OP之间的距离为
,OP之间的距离为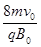 ,已知粒子最后能回到O点。
,已知粒子最后能回到O点。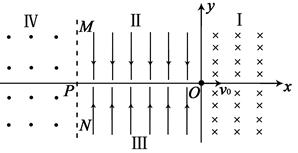
(1)带电粒子从O点飞出后,第一次回到x轴时的位置和时间;
(2)根据题给条件画出粒子运动的轨迹;
(3)带电粒子从O点飞出后到再次回到O点的时间。