已知
是等差数列，d为公差且不为0，a1和d均为实数，它的前n项和记作Sn，设集合
．试问下列命题是否是真命题，如果是真命题，请给予证明；如果是假命题，请举反例说明．
（1）若以集合A中的元素作为点的坐标，则这些点都在同一条直线上；
（2）
至多有一个元素；
（3）当a1≠0时，一定有
．
一个路口的红绿灯,红灯的时间为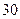
秒,黄灯的时间为
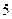秒,绿灯的时间为
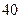秒,当你到达路口时看见下列三种情况的概率各是多少?
(1) 红灯 (2) 黄灯 (3)不是红灯
某路公共汽车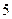
分钟一班准时到达某车站，求任一人在该车站等车时间少于
分钟的概率（假定车到来后每人都能上）
现有一批产品共有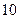
件，其中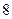
件为正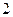品，
件为次品：
（1）如果从中取出一件，然后放回，再取一件，求连续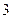
次取出的都是正品的概率；（2）如果从中一次取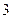件，求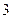件都是正品的概率．
从甲、乙、丙、丁四个人中选两名代表，求：
（１）甲被选中的概率
（２）丁没被选中的概率
已知定点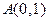
、
、
，动点
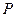满足：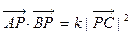
、
（1）求动点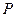的轨迹方程，并说明方程表示的图形；
（2）当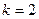
时，求
的最大值和最小值、