已知数列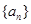
的前
项和为
且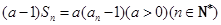
.
(1)求证数列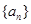是等比数列，并求其通项公式
；
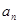(2)已知集合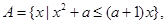
问是否存在实数
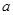，使得对于任意的
都有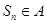
? 若存在，求出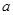的取值范围；若不存在，说明理由.
选修4—4：坐标系与参数方程
已知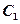
的极坐标方程为
，
分别为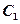在直角坐标系中与
轴，
轴
的交点。曲线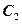
的参数方程为
（
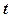为参数，且
），
为的中点，
（1）将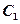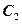，化为普通方程；
（2）求直线
（
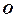为坐标原点）被曲线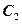所截得弦长。
选修4－1：几何证明选讲
如图，已知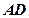
是
的外角
的平分线，交
的延长线于点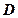
，延长
交的外接圆于点
，连结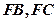
。
（1）求证：
；
（2）求证：
；
（3）若
是外接圆的直径，
且
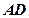，求的长。
（本小题满分12分）已知函数
，其中
为自然对数的底数，
。
（1）设
，求函数
的最值；
（2）若对于任意的
，都有
成立，
求
的取值范围。
（本小题满分12分）如图，已知三棱柱
的侧棱与底面垂直，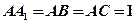
，
且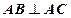
，
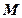是
的中点，
是
的中点，点
在
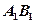上，
且满足
。
|
（1）证明：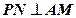
；
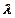取何值时，直线
与平面
所成的角
最大？并求该角最大值的
（本小题满分12分）某市十所重点中学进行高三联考，为了了解数学学科的考试情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：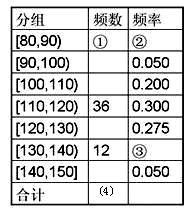
（1）根据上面频率分布表，求①，②，③，④处的数值；
（2）在所给的坐标系中画出区间
上的频率分布直方图；
（3）从样本在
的个体中任意抽取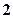
个个体，求至少有一个个体落在
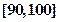的概率。