(本小题满分12分)
数列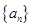 满足
满足
(1)求数列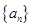 的通项公式;
的通项公式;
(2)令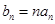 ,求数列的前n
,求数列的前n 项和
项和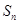
(本小题满分12分)
已知 是等比数列,
是等比数列,  ,
,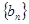 是等差数列,
是等差数列,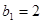
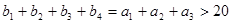
(1)求数列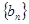 的通项公式;
的通项公式;
(2)求数列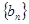 的前n项和
的前n项和 ;
;
(3)设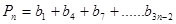 ,
, 其中n=1,2,......,试比较
其中n=1,2,......,试比较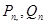 的大小。
的大小。
(本小题满分12分)
在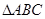 中,
中,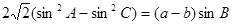 ,外接圆半径为
,外接圆半径为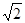 。
。
(1)求角C;
(2)求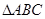 面积的最大值
面积的最大值
(满分12分)分已知函数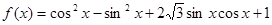 .
.
(1)求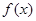 的最小正周期及
的最小正周期及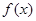 的最小值;
的最小值;
(2)若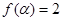 ,且
,且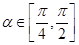 ,求
,求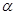 的值.
的值.
若二次项系数为a的二次函数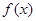 同时满足如下三个条件,求
同时满足如下三个条件,求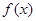 的解析式.
的解析式.
①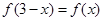 ;②
;②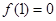 ;③对任意实数
;③对任意实数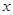 ,都有
,都有 恒成立.
恒成立.
(文) 设二次函数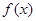 满足:(1)
满足:(1)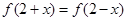 ,(2)被
,(2)被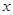 轴截得的弦长为2,(3)在
轴截得的弦长为2,(3)在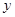 轴截距为6,求此函数解析式
轴截距为6,求此函数解析式