已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆右顶点到直线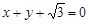 的距离为
的距离为 ,离心率
,离心率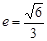
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知A为椭圆与y轴负半轴的交点,设直线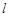 :
: ,是否存在实数m,使直线
,是否存在实数m,使直线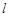 与椭圆有两个不同的交点M、N,是∣AM∣=∣AN∣,若存在,求出 m的值;若不存在,请说明理由。
与椭圆有两个不同的交点M、N,是∣AM∣=∣AN∣,若存在,求出 m的值;若不存在,请说明理由。
(本小题满分12分)
已知函数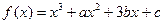 ,
, 且
且 为奇函数.
为奇函数.
(1)求 的值.
的值.
(2)求函数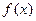 的单调区间
的单调区间
(本小题满分12分)
如图在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的
中点.
(1)求证: AC⊥BC1
(2)求证:AC1∥平面CDB1
(3)求异面直线AC1与B1C所成角的余弦值.
(本小题满分12分)
等比数列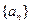 中,
中,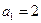 ,
, .
.
(1)求数列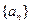 的通项公式.
的通项公式.
(2)若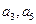 分别是等差数列
分别是等差数列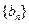 的第三项和第五项,试求数列
的第三项和第五项,试求数列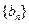 的通项
的通项
公式及前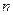 项和
项和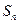 .
.
(本小题满分10分)
已知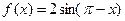 sin
sin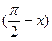 .
.
(1)求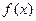 的最小正周期.
的最小正周期.
(2)若A,B,C是锐角△ABC的内角,其对边分别是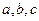 ,且
,且 ,
,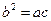
试判断△ABC的形状.
(Ⅰ)(Ⅱ)两道题普通班可以任意选择一道解答,实验班必做(Ⅱ)题
(Ⅰ)已知等比数列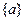 中,
中,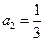 ,公比
,公比 。
。
(1)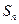 为
为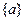 的前
的前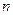 项和,证明:
项和,证明: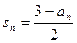
(2)设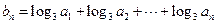 ,求数列
,求数列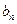 的通项公式.
的通项公式.
(Ⅱ)设正数数列{an}的前n项和为Sn满足Sn= (an+1)
(an+1)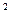 (n∈N*).
(n∈N*).
(1)求出数列{an}的通项公式。
(2)设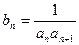 ,记数列{bn}的前n项和为
,记数列{bn}的前n项和为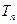 ,求
,求