(Ⅰ)(Ⅱ)两道题普通班可以任意选择一道解答,实验班必做(Ⅱ)题
(Ⅰ)已知等比数列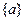 中,
中,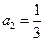 ,公比
,公比 。
。
(1)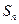 为
为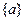 的前
的前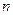 项和,证明:
项和,证明: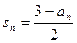
(2)设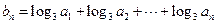 ,求数列
,求数列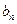 的通项公式.
的通项公式.
(Ⅱ)设正数数列{an}的前n项和为Sn满足Sn= (an+1)
(an+1)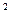 (n∈N*).
(n∈N*).
(1)求出数列{an}的通项公式。
(2)设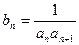 ,记数列{bn}的前n项和为
,记数列{bn}的前n项和为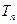 ,求
,求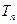
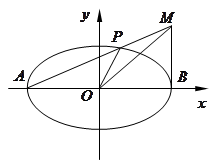
如图,已知椭圆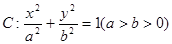 ,
,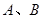 是长轴的左、右端点,动点
是长轴的左、右端点,动点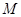 满足
满足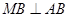 ,联结
,联结 ,交椭圆于点
,交椭圆于点 .
. 
(1)当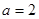 ,
,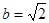 时,设
时,设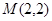 ,求
,求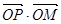 的值;
的值;
(2)若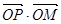 为常数,探究
为常数,探究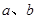 满足的条件?并说明理由;
满足的条件?并说明理由;
(3)直接写出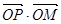 为常数的一个不同于(2)结论类型的几何条件.
为常数的一个不同于(2)结论类型的几何条件.
定义:设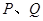 分别为曲线
分别为曲线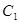 和
和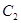 上的点,把
上的点,把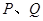 两点距离的最小值称为曲线
两点距离的最小值称为曲线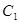 到
到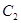 的距离.
的距离.
(1)求曲线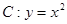 到直线
到直线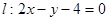 的距离;
的距离;
(2)若曲线 到直线
到直线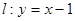 的距离为
的距离为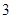 ,求实数
,求实数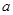 的值;
的值;
(3)求圆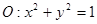 到曲线
到曲线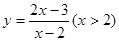 的距离.
的距离.
设正四棱锥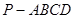 的侧面积为
的侧面积为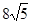 ,若
,若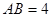 .
.
(1)求四棱锥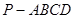 的体积;
的体积;
(2)求直线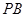 与平面
与平面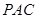 所成角的大小.
所成角的大小.
设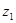 是方程
是方程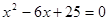 的一个根.
的一个根.
(1)求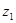 ;
;
(2)设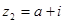 (其中
(其中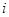 为虚数单位,
为虚数单位,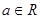 ),若
),若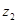 的共轭复数
的共轭复数 满足
满足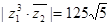 ,求
,求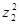 .
.
在直角坐标系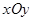 中,设动点
中,设动点 到定点
到定点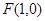 的距离与到定直线
的距离与到定直线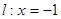 的距离相等,记
的距离相等,记 的轨迹为
的轨迹为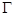 .又直线
.又直线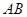 的一个方向向量
的一个方向向量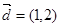 且过点
且过点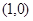 ,
,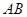 与
与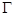 交于
交于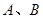 两点,求
两点,求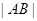 的长.
的长.