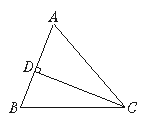
已知一个等腰三角形的底边和腰的长分别为12 cm和10 cm,求这个三角形的面积.
下图甲是任意一个直角三角形ABC,它的两条直角边的边长分别为a、b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b的正方形内.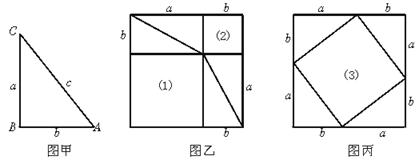
①图乙和图丙中(1)(2)(3)是否为正方形?为什么?
②图中(1)(2)(3)的面积分别是多少?
③图中(1)(2)的面积之和是多少?
④图中(1)(2)的面积之和与正方形(3)的面积有什么关系?为什么?
由此你能得到关于直角三角形三边长的关系吗?
请你观察下列图形,直角三角形ABC的两条直角边的长分别为AC=7,BC=4,请你研究这个直角三角形的斜边AB的长的平方是否等于42+72?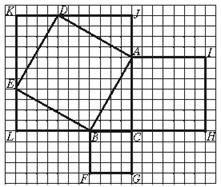
如下图,A、B两点都与平面镜相距4米,且A、B两点相距6米,一束光线由A射向平面镜反射之后恰巧经过B点.求B点到入射点的距离.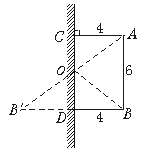
如下图所示,△ABC中,AB="15" cm,AC="24" cm,∠A=60°,求BC的长.