(本题9分)两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC="1." 固定△ABC不动,将△DEF进行如下操作:
(1)如图1,△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.
(2)如图2,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.
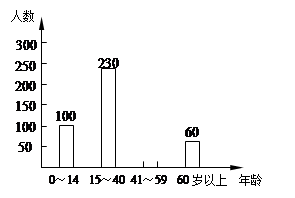 (3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinAED的值.
(3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinAED的值.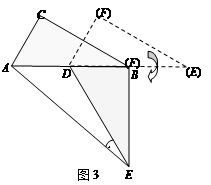
某地区随机抽取若干名八年级学生进行地理会考模拟测试,并对测试成绩(x分)进行了统计,具体统计结果见下表:
某地区八年级地理会考模拟测试成绩统计表
| 分数段 |
90<x≤100 |
80<x≤90 |
70<x≤80 |
60<x≤70 |
x≤60 |
| 人数 |
1200 |
1461 |
642 |
480 |
217 |
(1)填空:①本次抽样调查共测试了名学生;②参加地理会考模拟测试的学生成绩的中位数落在分数段上;③若用扇形统计图表示统计结果,则分数段为90<x≤100的人数所对应扇形的圆心角的度数为;
(2)该地区确定地理会考成绩60分以上(含60分)的为合格,要求合格率不低于97%.现已知本次测试得60分的学生有117人,通过计算说明本次地理会考模拟测试的合格率是否达到要求?
已知:如图,在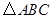 中,
中,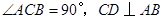 于点
于点 ,点
,点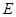 在
在 上,
上,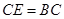 ,过
,过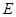 点作
点作 的垂线,交
的垂线,交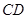 的延长线于点
的延长线于点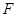 .求证:
.求证: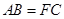 .
.
计算:
解方程:
如图,已知抛物线y=-x2+2x+3交x轴于A、B两点(点A在点B的左侧),与y轴交于点C。
(1)求点A、B、C的坐标。
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积。
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由。