(本小题满分12分)已知顶点在坐标原点,焦点在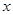 轴正半轴的抛物线上有一点
轴正半轴的抛物线上有一点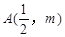 ,
, 点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设
点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设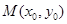 为抛物线上的一个定点,过
为抛物线上的一个定点,过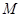 作抛物线的两条互相垂直的弦
作抛物线的两条互相垂直的弦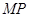 ,
,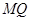 ,求证:
,求证: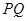 恒过定点
恒过定点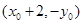 .(3)直线
.(3)直线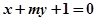 与抛物线交于
与抛物线交于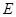 ,
,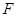 两点,在抛物线上是否存在点
两点,在抛物线上是否存在点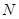 ,使得△
,使得△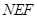 为以
为以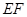 为斜边的直角三角形.
为斜边的直角三角形.
设平面内两定点 、
、 ,直线
,直线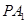 和
和 相交于点
相交于点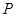 ,且它们的斜率之积为定值
,且它们的斜率之积为定值 。
。
(I)求动点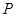 的轨迹
的轨迹 的方程;
的方程;
(II)设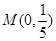 ,过点
,过点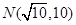 作抛物线
作抛物线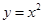 的切线交曲线
的切线交曲线 于
于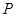 、
、 两点,求
两点,求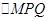 的面积。
的面积。
某项新技术进入试用阶段前必须对其中三项不同指标甲、乙、丙进行通过量化检测。假设该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为 ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
(Ⅰ)求该项技术量化得分不低于8分的概率;
(Ⅱ)记该技术的三个指标中被检测合格的指标个数为随机变量 ,求
,求 的分布列与数学期望。
的分布列与数学期望。
如图:C、D是以AB为直径的圆上两点, 在线段
在线段 上,且
上,且  ,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上.
,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上.
(I)求证平面ACD⊥平面BCD;
(II)求证:AD//平面CEF.
已知函数
(I)若 ,求sin2x的值;
,求sin2x的值;
(II)求函数 的最大值与单调递增区间.
的最大值与单调递增区间.
已知等差数列 的公差
的公差 ,它的前n项和为
,它的前n项和为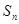 ,若
,若 且
且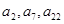 成等比数列.
成等比数列.
(I)求数列 的通项公式;
的通项公式;
(II)设数列 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn.