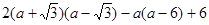如下图所示,已知直线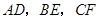 相交于
相交于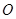 ,
,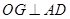 ,且
,且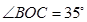 ,
,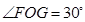 .求
.求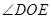 的度数.
的度数.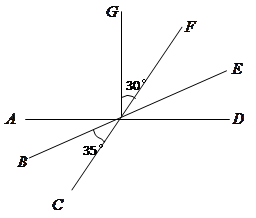
学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
如图所示的转盘,分成三个相同的扇形,指针位置固定转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,当作指向右边的扇形).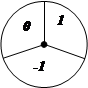
(1)求事件“转动一次,得到的数恰好是0”发生的概率;
(2)写出此情景下一个不可能发生的事件.
(3)用树状图或列表法,求事件“转动两次,第一次得到的数与第二次得到的数绝对值相等”发生的概率.
如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
求证: BE=DF;
(1)解方程: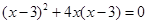
(2) 解不等式组
计算:
(1)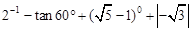
(2)