设椭圆的中心是坐标原点,焦点在x轴上,离心率 ,已知
,已知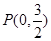 到这个椭圆上的点的最远距离为
到这个椭圆上的点的最远距离为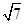 ,求这个椭圆方程,并求椭圆上到点P距离为
,求这个椭圆方程,并求椭圆上到点P距离为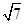 的点Q坐标.
的点Q坐标.
设函数f(x)=cos(2x+ )+sin
)+sin x.(1)求函数f(x)的最大值和最小正周期. w.w.(2)设A,B,C为
x.(1)求函数f(x)的最大值和最小正周期. w.w.(2)设A,B,C为 ABC的三个内角,若cosB=
ABC的三个内角,若cosB= ,
, ,且C为锐角,求sinA.
,且C为锐角,求sinA.
已知向量 ,向量,
,向量, 与向量
与向量 的夹角为
的夹角为 ,且
,且 ="-1" (1)求向量
="-1" (1)求向量 ; (2)设向量
; (2)设向量 =(1,0),向量
=(1,0),向量 ,其中0<
,其中0< <
<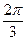 ,若
,若 =0,试求|
=0,试求| ︱的取值范围。
︱的取值范围。
已知向量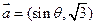 ,
,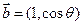 ,
,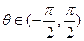 .(1)若
.(1)若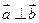 ,求
,求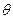 ;(2)求
;(2)求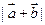 的最大值.
的最大值.
已知向量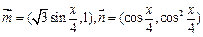 .(1)若
.(1)若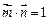 ,求
,求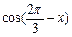 的值;(2)记
的值;(2)记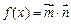 ,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
某班有48名同学,一次考试后数学成绩服从正态分布.平均分为80,标准差为10,问从理论上讲在80分至90分之间有多少人?