某工厂加工一批产品,为了提前完成任务,规定每个工人完成150个以内,按每个产品3元付报酬,超过150个,超过部分每个产品付酬增加0.2元;超过250个,超过部分出按上述规定外,每个产品付酬增加0.3元,求一个工人:
①完成150个以内产品得到的报酬y(元)与产品数x(个之间的函数关系式;
②完成150个以上,但不超过250个产品得到的报酬y(元)与产品数量x(个)的函数关系式;
③完成250个以上产品得到的报酬y(元)与产品数量x(个)的函数关系式.
马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50方向上,在救助船B的西北方向上,船B在船A正东方向140海里处。(参考数据:sin36.5≈0.6,cos36.5≈0.8,tan36.5≈0.75).
(1)求可疑漂浮物P到A、B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处。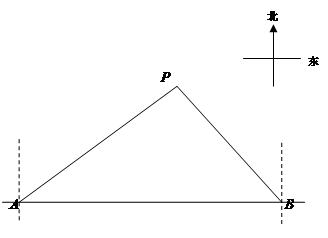
如图,一次函数y1=kx+b的图象与反比例函数y2=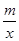 的图象相交于点A(2,5)和点B,与y轴相交于点C(0,7).
的图象相交于点A(2,5)和点B,与y轴相交于点C(0,7).
(1)求这两个函数的解析式;
(2)当x取何值时,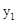 <
< .
.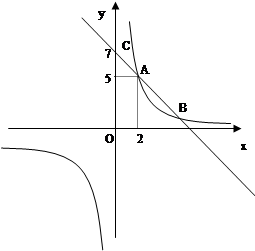
已知关于x的一元二次方程x2-2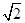 x+m=0,有两个不相等的实数根.
x+m=0,有两个不相等的实数根.
⑴求实数m的最大整数值;
⑵在⑴的条下,方程的实数根是x1,x2,求代数式x12+x22-x1x2的值.
在学习“二元一次方程组的解”时,数学张老师设计了一个数学活动. 有A、B 两组卡片,每组各3张,A组卡片上分别写有0,2,3;B组卡片上分别写有-5,-1,1.每张卡片除正面写有不同数字外,其余均相同.甲从A组中随机抽取一张记为x,乙从B组中随机抽取一张记为y.
(1)若甲抽出的数字是2,乙抽出的数是-1,它们恰好是ax-y=5的解,求a的值;
(2)求甲、乙随机抽取一次的数恰好是方程ax-y=5的解的概率.(请用树形图或列表法求解)
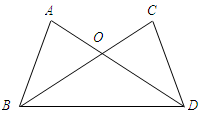
如图,AD、BC相交于O,OA=OC,∠OBD=∠ODB. 求证:AB=CD.