如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.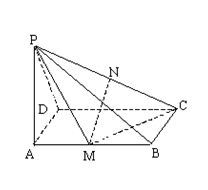
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD.
本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为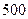 元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
在数列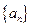 中,
中,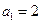 ,
,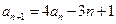 ,
, .
.
(1)证明数列 是等比数列; (2)求数列
是等比数列; (2)求数列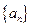 的前
的前 项和
项和 ;
;
(3) 证明不等式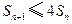 ,对任意
,对任意 皆成立.
皆成立.
(本小题满分14分)如图, 在矩形 中,
中,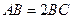 ,
, 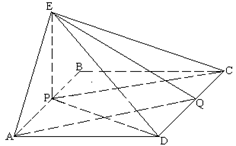
 分别为线段
分别为线段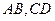 的中点,
的中点,  ⊥平面
⊥平面 .
.
(1) 求证: 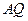 ∥平面
∥平面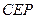 ;
;
(2) 求证:平面 ⊥平面
⊥平面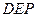 ;
;
(3) 若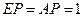 , 求三棱锥
, 求三棱锥 的
的
体积.
(本小题满分12分)已知函数 (x>0)在x = 1处取得极值
(x>0)在x = 1处取得极值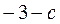 ,其中a,b,c为常数。
,其中a,b,c为常数。
(1)试确定a,b的值; (2) 讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式 恒成立,求c的取值范围。
恒成立,求c的取值范围。
(本小题满分12分)已知: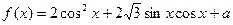 ,
,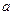 为实常数.
为实常数.
(1) 求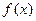 的最小正周期;
的最小正周期;
(2)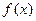 在
在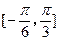 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求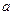 的值.
的值.