(本小题满分12分)
福州市某大型家电商场为了使每月销售空调和冰箱获得的总利润达到最大,对某月即将出售的空调和冰箱进行了相关调查,得出下表:
| 资金 |
每台空调或冰箱所需资金 (百元) |
月资金最多供应量 (百元) |
|
| 空调 |
冰箱 |
||
| 进货成本 |
30 |
20 |
300 |
| 工人工资 |
5 |
10 |
110 |
| 每台利润 |
6 |
8 |
|
问:该商场如果根据调查得来的数据,应该怎样确定空调和冰箱的月供应量,才能使商场获得的总利润最大?总利润的最大值为多少元?
(本小题满分15分)在 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)当 取得最大值时,试判断
取得最大值时,试判断 的形状.
的形状.
(本题满分14分)设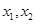 为函数
为函数 两个不同零点.
两个不同零点.
(Ⅰ)若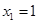 ,且对任意
,且对任意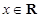 ,都有
,都有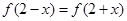 ,求
,求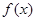 ;
;
(Ⅱ)若 ,则关于
,则关于 的方程
的方程 是否存在负实根?若存在,求出该负根的取值范围,若不存在,请说明理由;
是否存在负实根?若存在,求出该负根的取值范围,若不存在,请说明理由;
(Ⅲ)若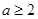 ,
,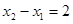 ,且当
,且当 时,
时, 的最大值为
的最大值为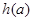 ,求
,求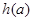 的最小值.
的最小值.
设各项均为正数的等比数列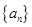 的公比为
的公比为 ,
,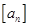 表示不超过实数
表示不超过实数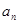 的
的
最大整数(如 ),设
),设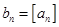 ,数列
,数列 的前
的前 项和为
项和为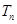 ,
,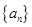 的前
的前 项和为
项和为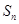 .
.
(Ⅰ)若 ,求
,求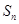 及
及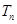 ;
;
(Ⅱ)若对于任意不超过2015的正整数 ,都有
,都有 ,证明:
,证明: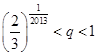 .
.
(本题满分15分)已知椭圆 :
: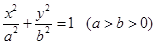 过点
过点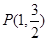 ,离心率为
,离心率为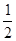 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设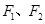 分别为椭圆
分别为椭圆 的左、右焦点,过
的左、右焦点,过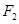 的直线
的直线 与椭圆
与椭圆 交于不同两点
交于不同两点 ,记
,记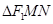 的内切圆的面积为
的内切圆的面积为 ,求当
,求当 取最大值时直线
取最大值时直线 的方程,并求出最大值.
的方程,并求出最大值.
如图,在四棱锥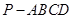 中,底面
中,底面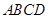 是平行四边形,
是平行四边形, 平面
平面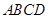 ,点
,点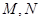 分别为
分别为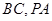 的中点,且
的中点,且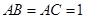 ,
, .
.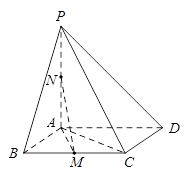
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)设直线 与平面
与平面 所成角为
所成角为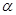 ,当
,当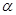 在
在 内变化时,求二面角
内变化时,求二面角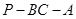 的取值范围.
的取值范围.